Beslissingsbomen#

Inleiding#

Een beslissingsbomen is een grafisch hulpmiddel dat gebruikt kan worden om besluitvorming te faciliteren. Er bestaan meerdere Machine Learning algoritmes die beslissingsbomen kunnen produceren op basis van een trainingset van voorbeelden. Hoe dit in zijn werk gaat, wordt uitgelegd in dit hoofdstuk. Eens de beslissingsboom geconstrueerd is, kan hij gebruikt worden als model om bijvoorbeeld de classificatie te kunnen doen van nieuwe en ongeclassificeerde instanties. Dit heeft heel veel praktische toepassingen gaande van het voorspellen van interessante tijdstippen om aandelen te kopen, het bepalen of iemand kredietwaardig is bij het afsluiten van een lening, het detecteren van tumoren in foto’s, het voorspellen van de slaagkans van studenten Data Science 1, …

Elke rij in een trainingset wordt ook wel een instantie (Engels: instance) genoemd. In sommige trainingsets zullen deze instanties een extra kolom hebben waarvan de waarden fungeren als labels voor die instanties. Wanneer een algoritme gebruik maakt van deze gelabelede instanties om van te leren, spreken we van supervised learning. Het algoritme (ID3) dat we in dit hoofdstuk bestuderen, is dus een vorm van supervised learning. In het hoofdstuk over Clustering zullen we het hebben over unsupervised learning, daar zullen de instanties geen labelkolom hebben en zullen we dus op een andere manier moeten leren van de voorbeelden in onze trainingset.

Geschiedenis#

Al in de jaren 70 van de vorige eeuw werden de grondbeginselen van beslissingsbomen door Breiman gelegd [BFSO84]. Het bekendste algoritme om beslissingsbomen te maken, ID3 genaamd, is van de hand van Quinlan [Qui86]. Later, in de jaren 90 heeft Quinlan dit algoritme verbeterd onder de naam C4.5, zodat het ook toegepast kon worden op continue gegevens, en op gegevens met ontbrekende waarden (Engels: missing values)[Sal94].

In dit hoofdstuk bestuderen we dus wat een beslissingsboom juist is, en leren we hoe we een beslissingsboom kunnen opstellen m.b.v. het ID3 algoritme vertrekkende van een verzameling traininggegevens.

Wat zijn beslissingsbomen?#

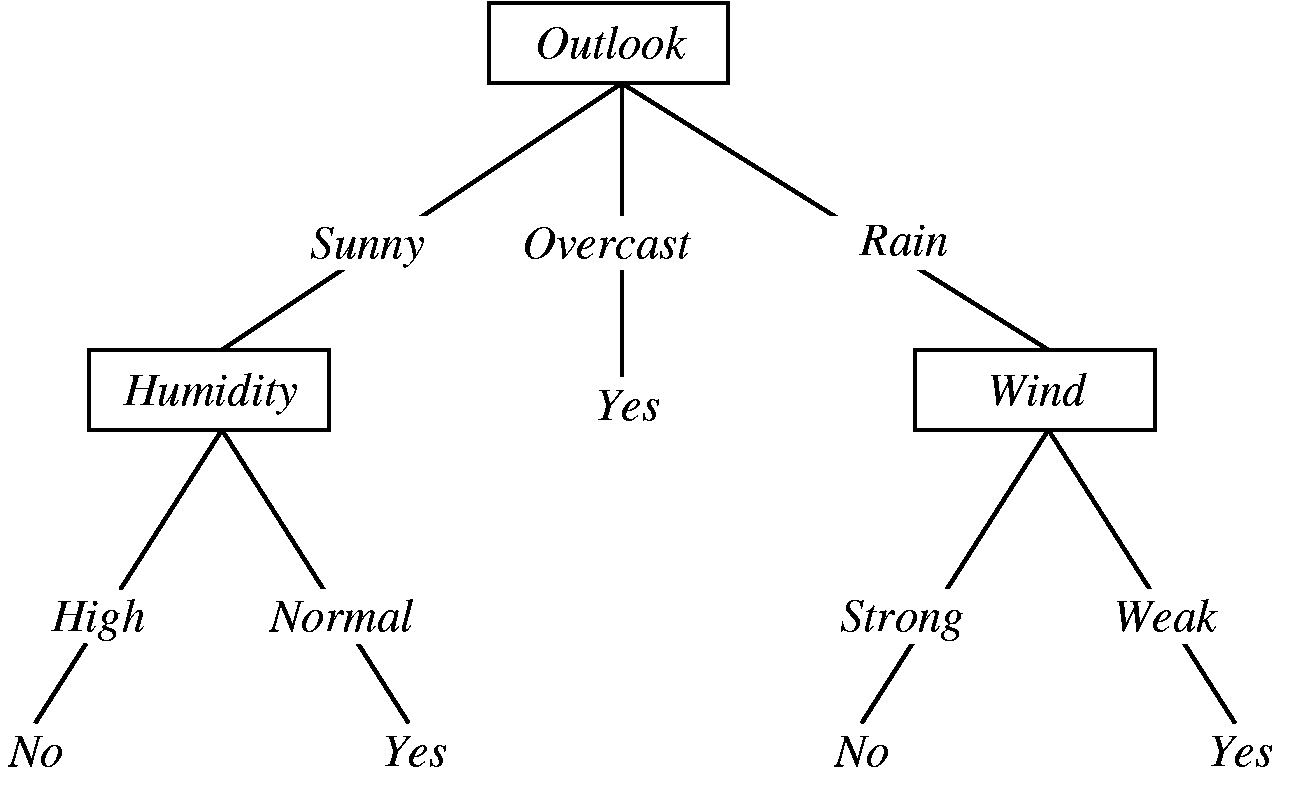
Zoals het woord beslissingsboom laat uitschijnen, is het een boom-achtige structuur die echter ondersteboven staat en die bestaat uit knooppunten die verbonden zijn door benoemde pijlen (zie Figuur 1. Elk knooppunt stemt overeen met een plaats waar een beslissing genomen moet worden. De uiteinden van een beslissingsbomen zijn knooppunten zonder vertrekkende pijlen en deze worden bladknooppunten genoemd (in Figuur 1 hebben deze de labels ‘Yes’ en ‘No’ zonder kader). Elk knooppunt bevat de naam van een eigenschap (Engels: attribute) van de gegevens op basis waarvan voorbeelden kunnen gescheiden worden van elkaar. Een bladknooppunt bevat de uitkomst (Engels: target) waartoe het voorbeeld behoort. Het target is gelijk aan een waarde uit de labelkolom (target attribute).

Figuur 1

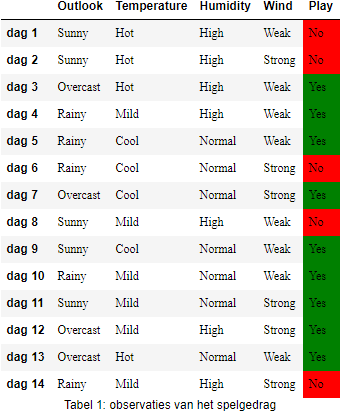
In Figuur 1 zie je een voorbeeld van een in de literatuur wèl heel bekende beslissingsboom. Deze beslissingsboom is het resultaat van de toepassing van het ID3 algoritme op deze traininggegevens waarbij onderzocht of een persoon een bepaald spel (bv. Tennis) gaat spelen in funtie van de weeromstandigheden:

We kunnen deze beslissingsboom ook vinden m.b.v. een Python library en dan ziet deze er zo uit:

import graphviz
from id3.export import DotTree
from id3 import Id3Estimator, export_graphviz

attributen = weather_nominal.drop(columns=['Play'])
target = weather_nominal.Play
X = attributen.to_numpy().tolist()
y = target.to_numpy().tolist()

model = Id3Estimator()
model.fit(X, y)

model_tree = DotTree()
export_graphviz(model.tree_, model_tree, feature_names=attributen.columns)
graphviz.Source(model_tree.dot_tree)

Het doel van deze beslissingsboom is om te bepalen of een persoon zal gaan sporten (kolom $P l a y$ ) op basis van weerkenmerken (kolommen $O u t l o o k$ , $T e m p e r a t u r e$ , $H u m i d i t y$ en $W i n d$ ) van de dag. We willen dus kunnen voorspellen wat de waarde van het targetattribuut ‘Play’ (met waarden ‘Yes’ of ‘No’) zal zijn op basis van de overige attributen ( $O u t l o o k$ , $T e m p e r a t u r e$ , $H u m i d i t y$ en $W i n d$ ) van een dag. Het ID3 algoritme leert de verborgen kennis in deze tabel en bouwt er een model van. Dat model kan dan gebruikt worden om te bepalen of iemand zal gaan sporten op een toekomstige dag (15, 16, …) door enkel gebruik te maken van de overige eigenschappen van die dagen.

Merk op dat alle eigenschappen in dit voorbeeld een nominaal of ordinaal meetniveau hebben, maar in het algemene geval hoeft dit niet zo te zijn. Merk ook op dat alle instanties in Tabel 1 gelabelde instanties zijn, namelijk het Play-kenmerk is door een ‘leraar’ toegevoegd aan deze training-dataset, zodat een ‘leerling’ (hier het ID3 algoritme) het verband tussen de overige kenmerken en het labelkenmerk kan leren (i.e., supervised learning).

Het ID3 algoritme#

Je vraagt nu waarschijnlijk af hoe je zo’n beslissingsboom kan opstellen? De pseudo-code hieronder geeft een aantal stappen om dit probleem op te lossen en sommige van die stappen vergen op hun beurt weer een aantal onderliggende stappen (zoals de verwijzing naar Information Gain en Entropie in stappen 1 en Stap 2d waarover zo dadelijk meer):

Bovenstaand algoritme is bekend onder de naam Iterative Dichotomiser 3 (ID3) en op regel 10 kan je duidelijk zien dat het hier gaat om een recursief algoritme, want het roept zichzelf op. Je roept dit algoritme aan met een tabel van gegevens $S$ en een lege boomdatastructuur. In de stappen van het algoritme maken we op regels 2 en 9 gebruik van een aantal hulpfuncties, genaamd information gain (IG) en entropie (E). Deze twee belangrijke hulpfuncties worden in latere paragraaf toegelicht. Zij vormen het hart van het eigenlijk algoritme en moeten dus grondig bestudeerd worden.

Het ID3 algoritme werkt alleen voor gegevens van meetniveau’s die nominaal of ordinaal zijn. Als je toch gegevens hebt op een hoger niveau zoals interval of ratio dan zal je eerst klassen moeten aanmaken of de verbeterde versie van het ID3-algoritme, genaamd C4.5, moeten gebruiken, waarover later meer. Een andere term voor het aanmaken van klassen is discretiseren; in softwarepakketten kom je vaak deze laatste benaming tegen. In Python kan je discretiseren m.b.v. de pd.cut - functie. Eens al je eigenschappen gediscretiseerd zijn kan je weer gebruik maken van het ID3 algoritme om een beslissingsboom op te stellen.

Voorbeeld

selecteer eigenschap ‘Outlook’
maak een knooppunt met naam ‘Outlook’ en teken drie benoemde pijlen die vertrekken van uit het knooppunt: een pijl met ‘Overcast’, met ‘Rainy’ en met ‘Sunny’ ernaast .

Door de ‘pijlen te volgen’ bekomen we drie deelverzamelingen (kindtabellen) van de oorspronkelijke verzameling van gegevens:

a. Kindtabel Overcast met daarin dag 3, dag 7, dag 12, dag 13 b. Kindtabel Rainy met daarin dag 4, dag 5, dag 6, dag 10, dag 14 c. Kindtabel Sunny met daarin dag 1, dag 2, dag 8, dag 9, dag 11
we herhalen stappen 1 en 2 voor alle deelverzamelingen (a) t.e.m. (c).
we stoppen het algoritme voor deelverzameling 2 want deze hebben allen dezelfde uitkomst ‘Yes’

In het bovenstaande algoritme hebben we wel nog verzwegen hoe we de beste eigenschap konden selecteren. Er zijn verschillende manieren waarop de ‘beste’ eigenschap geselecteerd kan worden. We bekijken in de volgende paragraaf één van de meeste bekende technieken die gebaseerd is op de begrippen entropie en information gain.

Entropie en information gain#

Zoals aangehaald in de vorige paragraaf zijn entropie en information gain twee belangrijke hulpfuncties die het ID3 algoritme zijn kracht geven. Omdat information gain op zijn beurt gebaseerd is op entropie lichten we eerst toe wat Entropie is.

Entropie#

De entropie van een tabel van gegevens $S$ is een maat voor de zuiverheid van de gegevens in de tabel, gemeten met een bepaalde eigenschap uit die tabel in gedachten. Als je het ID3 algoritme van hierboven nog eens herleest, zal je merken dat de stop-conditie op regel 9 gebaseerd is op entropie: je stopt met het uitbreiden van de beslissingsboom wanneer ‘allen dezelfde uitkomst hebben’, m.a.w. je gaat verder wanneer een subtabel nog niet helemaal zuiver is. Entropie is niets anders dan een functie (zowel wiskundig als programmatorisch) die ons, op basis van een wiskundige formule, een getal zal teruggeven dat een maat is voor de zuiverheid van de gegevens in $S$ .

Definitie:

E (S) = \sum_{v \in A} - \frac{| S_{A = v} |}{| S |} \cdot l o g_{2} \frac{| S_{A = v} |}{| S |}

Deze wiskundige formule ziet er nogal indrukwekkend uit, maar in feite is ze veel eenvoudiger dan ze laat uitschijnen. We bekijken de verschillende onderdelen en passen ze toe op ons weer-voorbeeld. Eerst moeten we begrijpen waarvoor elk symbool staat:

$E$ staat voor entropie. Dit is een getal tussen 0 en 1 dat aangeeft hoe zuiver de verzameling $S$ van gegevens is, 0 komt overeen met een helemaal zuivere verzameling en 1 met een maximaal onzuivere verzameling.
$A$ staat voor attribuut of eigenschap. Dit is het attribuut waarvan we de zuiverheid willen berekenen, bijvoorbeeld $A = P l a y$ of $A = O u t l o o k$
$v$ staat voor value. Het is in feite een variabele die alle waarden van $A$ kan aannemen. In het geval van $A = P l a y$ kan $v$ de waarden ‘Yes’ en ‘No’ aannemen.
$S$ is de verzameling (van het Engelse set) van gegevens. Dit is niets anders dan een tabel van gegevens. Het algoritme begint steeds met de oorspronkelijke set van gegevens (zie Tabel 1)
$| S_{A = v} |$ is het aantal (de $| | - o p e r a t o r$ ) instanties van de verzameling S (=rijen van Tabel 1) die de waarde $v$ hebben voor attribuut $A$ .
$| S |$ is het totaal aantal instanties (het totaal aantal rijen in de tabel)

Nu we een beter idee hebben wat de entropieformule inhoudt kunnen we deze nu concreet toepassen voor de berekening van de entropie van de gegevens S waarbij we ‘Play’ als het target attribuut beschouwen.

E (S) = \sum_{v \in {Y e s, N o}} - \frac{| S_{A = v} |}{| S |} \cdot l o g_{2} \frac{| S_{A = v} |}{| S |}

\begin{matrix} = - \frac{9}{14} \cdot l o g_{2} \frac{9}{14} - \frac{5}{14} \cdot l o g_{2} \frac{5}{14} \end{matrix}

\begin{matrix} = 0.940 \end{matrix}

De waarde die we vinden ligt dicht tegen één, maar wat betekent dit nu?

Dit betekent dat de het attribute $P l a y$ zeer onzuiver is, of nog dat de wanorde groot is. Het kon allemaal nog een tikkeltje wanordelijker geweest zijn, mochten er evenveel dagen zijn waarop er gesport wordt als dat er dagen zijn dat er niet gesport wordt, want dan zou de entropie van ‘Play’ zelfs precies 1 geweest zijn (reken dit eens na).

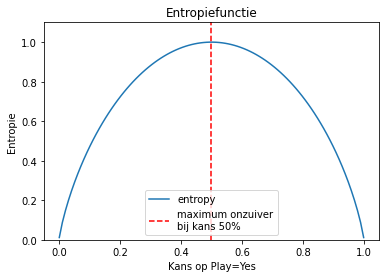
De entropiecurve in Figuur 4 toont hoe de entropie van een binaire variabele (een binaire variabele is een toevalsveranderlijke die slechts twee waarden kan aannemen) zoals ‘Play’ toeneemt tot één wanneer de kans op de beide waarden 0.5 wordt.

In het geval van het ‘Play’-attribuut is de kans op $P (P l a y = Y e s) = \frac{9}{14} = 0.64$ en er is dus een iets hogere kans op ‘Yes’ dan op ‘No’. Dit wordt dan ook gereflecteerd in de berekende waarde van $E (S)$ die net iets lager is dan één.

We moeten nu op één of andere manier de informatie die deze entropie-berekening ons geeft kunnen gebruiken om via een aantal belissingen te komen tot steeds ‘zuiverwordende’ subtabellen van Tabel 1 totdat deze subtabellen helemaal zuiver zijn en enkel nog maar óf ‘No’ óf ‘Yes’ hebben staan bij hun ‘Play’-attribuut (je kan dit zelf al testen door de beslissingsboom uit Figuur 1 toepassen op de weergegevens en dan zal je zien dat je na een aantal belissingen inderdaad overblijft met zuivere subtabellen). Hoe we dat aanpakken, bekijken we in de volgende paragraaf met het begrip information gain.

Information Gain#

Met de information gain (IG) zullen voor elk attribuut kunnen quantificeren wat de winst zal zijn qua ‘zuiverheidstoename’ als we de gegevens zouden splitsen op basis van de waarden van dat attribuut. Hoe hoger de information gain voor een bepaald attribuut des te beter. We geven eerst de formele definitie van information gain van een attribuut A.

Definitie:

I G (A) = E (S_{o u d e r}) - \sum_{v \in A} \frac{| S_{k i n d, v} |}{| S_{o u d e r} |} \cdot E (S_{k i n d, v})

Deze formule ziet er wederom een beetje indrukwekkend uit, maar ook hier geldt weer dat het eigenlijk allemaal niet zo moeilijk is. Deze formule heeft een intuitieve betekenis die het makkelijker maakt om ze te begrijpen: de information gain is gelijk aan de onzuiverheid $E (S_{o u d e r})$ van de originele tabel $S_{o u d e r}$ verminderd met het gewogen gemiddelde van de onzuiverheden $E (S_{k i n d, v})$ van de ontstane kindtabellen $S_{k i n d, v}$ . Het gewogen gemiddelde ontstaat doordat je het aantal rijen $| S_{k i n d, v} |$ van elke kindtabel afweegt t.o.v. van het totaal aantal rijen $| S_{o u d e r} |$ in de oudertabel.

In de volgende paragraaf zullen we dit helemaal wiskundig uitspitten, en zal bovenstaande formule duidelijker worden, maar om de berekeningswijze van information gain en het nut ervan goed te begrijpen is het belangrijk dat je nu goed begrijpt wat het ID3 algoritme inhoudt. We willen een tabel $S$ met gegevens gebruiken om een beslissingsboom op te stellen. Omdat het een recursief algoritme is, zullen we bij elke recursieve oproep te maken hebben met een oudertabel $S_{o u d e r}$ en een aantal kindtabellen $S_{k i n d, v}$ (bekijk het ID3-Algoritme nog eens op pagina ).

De eerste oudertabel is de uiteraard de originele tabel $S$ met gegevens zoals bijvoorbeeld die uit Tabel 1. Voor elk attribuut $A$ waarvoor je de information gain gaat berekenen zullen kindtabellen ontstaan: één kindtabel per waarde $v$ die het attribuut $A$ kan aannemen. Pas wanneer alle information gains berekend zijn, kan de splitsing van de tabel gebeuren op basis van het attribuut met de grootste information gain. Na al die berekeningen hebben enkel nog maar ‘stap 1’ uit het ID3-algoritme uitgevoerd!

De kindtabellen $S_{k i n d, v}$ die dan ontstaan zullen op hun beurt gaan dienen als oudertabel (regel 10) en het algoritme stopt pas als alle kindtabellen zuiver zijn. Met andere woorden zolang er nog één kindtabel niet zuiver is, wordt het een oudertabel en gaat het splitsen door (regel 9 en 10).

ID3 toegepast#

We beschikken nu over alle puzzelstukjes om het ID3-algoritme te gaan toepassen op de tabel met de weergegevens (Tabel 1). Zoals je zal merken vergt dit heel veel berekeningen, die wel gelukkig door onze (voorlopige) trouwe slaaf, de computer, kunnen laten oplossen, maar het is belangrijk dat je ook goed begrijpt hoe dit allemaal in zijn werk gaat.

De stappen die we hieronder beschrijven zijn de stappen uit het ID3-algoritme. We gaan ervan uit dat we een lege boomstructuur hebben zonder ‘root node’.

We beginnen bij stap 1.

Stap 1#

We moeten in deze stap bepalen welke node we bovenaan in de de boomstructuur zullen plaatsen. Daarom berekenen we de information gains voor attributen Outlook, Temperature, Humidity en Wind.

Outlook#

Op basis van de weergegevens kan je voor het attribuut ‘Outlook’ drie kindtabellen construeren: één voor elke waarde die het attribuut ‘Outlook’ kan aannemen.

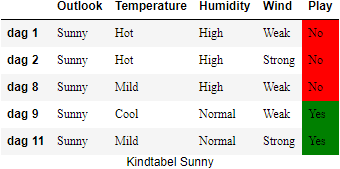
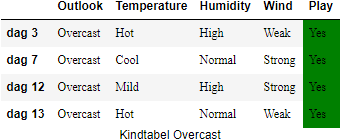
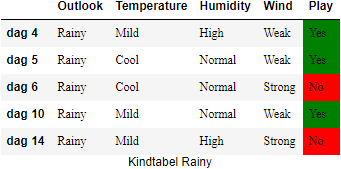
We moeten in deze stap bepalen welke node we bovenaan in de de boomstructuur zullen plaatsen. Daarom berekenen we de information gains voor attributen $O u t l o o k$ , $T e m p e r a t u r e$ , $H u m i d i t y$ en $W i n d$ .

Om de information gain $I G (O u t l o o k)$ van het attribuut $O u t l o o k$ te kunnen bereken en moeten nu eerst voor elk van deze kindtabellen de entropie $E (S_{k i n d, v})$ berekenen met formule van de entropie. We berekenen dus de entropie-waarden voor alle kindtabellen als volgt:

$E (S_{k i n d, S u n n y}) = \sum_{v \in {Y e s, N o}} - \frac{| S_{A = v} |}{| S |} \cdot l o g_{2} \frac{| S_{A = v} |}{| S |}$

$= - \frac{2}{5} \cdot l o g_{2} \frac{2}{5} - \frac{3}{5} \cdot l o g_{2} \frac{3}{5}$

$= 0.971$

$E (S_{k i n d, O v e r c a s t}) = \sum_{v \in {Y e s, N o}} - \frac{| S_{A = v} |}{| S |} \cdot l o g_{2} \frac{| S_{A = v} |}{| S |}$

$= - \frac{4}{4} \cdot l o g_{2} \frac{4}{4} - \frac{0}{4} \cdot l o g_{2} \frac{0}{4}$

$= 0$

$E (S_{k i n d, R a i n y}) = \sum_{v \in {Y e s, N o}} - \frac{| S_{A = v} |}{| S |} \cdot l o g_{2} \frac{| S_{A = v} |}{| S |}$

$= - \frac{3}{5} \cdot l o g_{2} \frac{3}{5} - \frac{2}{5} \cdot l o g_{2} \frac{2}{5}$

$= 0.971$

Eerder berekenden we al de entropie van de oudertabel $E (S_{o u d e r})$ , die we ook nodig hebben voor de berekening van $I G (O u t l o o k)$ . Onze oudertabel is redelijk onzuiver ( $E = 0.940$ ) en na splitsing op het attribuut ‘Outlook’ bekomen we drie kindtabellen waarvan er twee nog erg onzuiver zijn, $E (S_{k i n d, S u n n y}) = E (S_{k i n d, R a i n y}) = 0.971$ , en ééntje die perfect zuiver is $E (S_{k i n d, O v e r c a s t}) = 0$ .

Door het gewogen gemiddelde van deze entropies te berekenen van de bekomen kindtabellen bekomen we dus één getal dat de kwaliteit van deze splitsing karateriseert in termen van zuiverheid.

Wat is nu die ‘zuiverheidsgraad-verbetering’ die we zouden bekomen door de originele tabel op te splitsen in deze drie kindtabellen? Wel, dat hangt natuurlijk af van hoe groot elke kindtabel is. Je voelt intuitief aan dat elke kindtabel een groter aandeel zou moeten krijgen in de totale ‘zuiverheidsgraad-verbetering’ wanneer dit een grote deeltabel is dan wanneer het maar een klein tabelletje is van één rij. En de grootte van de kindtabel is natuurlijk relatief ten opzichte van de grootte $| S_{o u d e r} |$ van de originele oudertabel $S_{o u d e r}$ . Vandaar dat we formule in de formule van de information gain het aantal elementen van elke kindtabel $| S_{k i n d, v} |$ verhouden tot het aantal elementen in de ouder tabel $| S_{o u d e r} |$ .

$E_{g e m_k i n d t a b e l} = \frac{5}{14} \cdot E (S_{k i n d, S u n n y}) + \frac{4}{14} \cdot E (S_{k i n d, O v e r c a s t}) + \frac{5}{14} \cdot E (S_{k i n d, R a i n y})$

Door het verschil te maken van de originele zuiverheid $E (S_{o u d e r})$ en de gewogen samengestelde zuiverheid $E_{g e m_k i n d t a b e l}$ van de kindtabellen, bekomen we dus inderdaad een getal dat ons meedeelt hoeveel ‘zuiverheidsverbetering’ er zal plaats optreden als we zouden splitsen op dat attribuut.

$I G (O u t l o o k) = zuiverheid oudertabel - gewogen zuiverheid van de kindtabellen$

$= E (S_{o u d e r}) - \sum_{v \in {S u n n y, O v e r c a s t, r a i n}} \frac{| S_{k i n d, v} |}{| S_{o u d e r} |} \cdot E (S_{k i n d, v})$

$= E (S_{o u d e r}) - \frac{5}{14} \cdot E (S_{k i n d, S u n n y}) - \frac{4}{14} \cdot E (S_{k i n d, O v e r c a s t}) - \frac{4}{14} \cdot E (S_{k i n d, R a i n y})$

$= 0.940 - \frac{5}{14} \cdot 0.971 - \frac{4}{14} \cdot 0 - \frac{5}{14} \cdot 0.971$

$= 0.246$

We moeten al deze berekeningen nu herhalen voor de resterende attributen $T e m p e r a t u r e$ , $H u m i d i t y$ en $W i n d$ en dat is behoorlijk wat werk waar met een Python library gelukkig wel een mouw kunnen aan aanpassen.

Temperature#

We creeëren eerst de kindtabellen voor het attribuut $T e m p e r a t u r e$ door ze te groeperen naar de drie waarden $H o t$ , $M i l d$ en $C o o l$ .

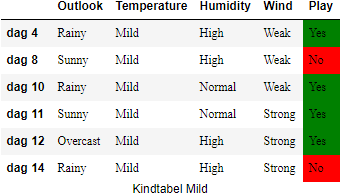
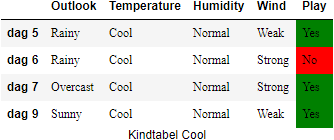
Nu berekenen we de entropiewaarden voor deze kindtabellen. Deze zijn een maat voor hoe zuiver het attribuut $T e m p e r a t u r e$ de originele gegevens kan krijgen.

$E (S_{k i n d, h o t}) = \sum_{v \in {Y e s, N o}} - \frac{| S_{A = v} |}{| S |} \cdot l o g_{2} \frac{| S_{A = v} |}{| S |}$

$= - \frac{2}{4} \cdot l o g_{2} \frac{2}{4} - \frac{2}{4} \cdot l o g_{2} \frac{2}{4}$

$= 1$

$E (S_{k i n d, m i l d}) = \sum_{v \in {Y e s, N o}} - \frac{| S_{A = v} |}{| S |} \cdot l o g_{2} \frac{| S_{A = v} |}{| S |}$

$= - \frac{4}{6} \cdot l o g_{2} \frac{4}{6} - \frac{2}{6} \cdot l o g_{2} \frac{2}{6}$

$= 0.918$

$E (S_{k i n d, c o o l}) = \sum_{v \in {Y e s, N o}} - \frac{| S_{A = v} |}{| S |} \cdot l o g_{2} \frac{| S_{A = v} |}{| S |}$

$= - \frac{3}{4} \cdot l o g_{2} \frac{3}{4} - \frac{1}{4} \cdot l o g_{2} \frac{1}{4}$

$= 0.811$

Nu we de entropiewaarden van de kindtabellen kennen, kunnen we de information gain van $T e m p e r a t u r e$ , $I G (T e m p e r a t u r e)$ , gaan berekenen.

Nu kunnen we ook de Information Gain voor $T e m p e r a t u r e$ berekenen:

$I G (T e m p e r a t u r e) = E (S_{o u d e r}) - \sum_{v \in {h o t,, m i l d, c o o l}} \frac{| S_{k i n d, v} |}{| S_{o u d e r} |} \cdot E (S_{k i n d, v})$

$= E (S_{o u d e r}) - \frac{4}{14} \cdot E (S_{k i n d, h o t}) - \frac{6}{14} \cdot E (S_{k i n d, m i l d}) - \frac{4}{14} \cdot E (S_{k i n d, c o o l})$

$= 0.940 - \frac{4}{14} \cdot 1 - \frac{6}{14} \cdot 0.918 - \frac{4}{14} \cdot 0.811$

$= 0.029$

De $I G (T e m p e r a t u r e)$ is minder goed dan dan de $I G (O u t l o o k)$ . Voorlopig blijft $O u t l o o k$ dus het attribuut waarop we eerst zouden splitsen. We onderzoeken nu het volgende attribuut $H u m i d i t y$ .

Humidity#

We construeren weer eerst de twee kindtabellen op basis van de waarden $H i g h$ en $N o r m a l$ van het attribuut $H u m i d i t y$ .

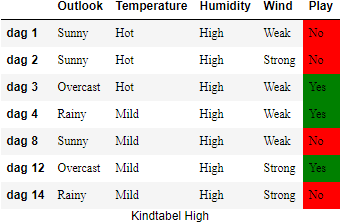
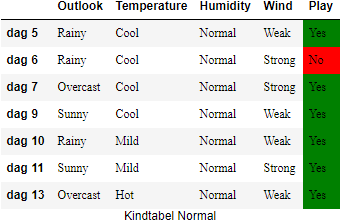
En de bijhorende entropiewaarden zijn:

$E (S_{k i n d, h i g h}) = \sum_{v \in {Y e s, N o}} - \frac{| S_{A = v} |}{| S |} \cdot l o g_{2} \frac{| S_{A = v} |}{| S |}$

$= - \frac{3}{7} \cdot l o g_{2} \frac{3}{7} - \frac{4}{7} \cdot l o g_{2} \frac{4}{7}$

$= 0.985$

$E (S_{k i n d, n o r m a l}) = \sum_{v \in {Y e s, N o}} - \frac{| S_{A = v} |}{| S |} \cdot l o g_{2} \frac{| S_{A = v} |}{| S |}$

$= - \frac{6}{7} \cdot l o g_{2} \frac{6}{7} - \frac{1}{7} \cdot l o g_{2} \frac{1}{7}$

$= 0.592$

$I G (H u m i d i t y) = E (S_{o u d e r}) - \sum_{v \in {h i g h, n o r m a l}} \frac{| S_{k i n d, v} |}{| S_{o u d e r} |} \cdot E (S_{k i n d, v})$

$= E (S_{o u d e r}) - \frac{7}{14} \cdot E (S_{k i n d, h i g h}) - \frac{7}{14} \cdot E (S_{k i n d, n o r m a l})$

$= 0.940 - \frac{7}{14} \cdot 0.985 - \frac{7}{14} \cdot 0.592$

$= 0.152$

Nog steeds blijft de IG van $O u t l o o k$ de beste tot nog toe. We controleren tenslotte voor het laatste attribuut $W i n d$ of dit nog een betere IG kan opleveren.

Wind#

We maken weer voor elke waarde die $W i n d$ kan aannemen een kindtabel. Dat zijn er dus twee, voor $W e a k$ en $S t r o n g$ .

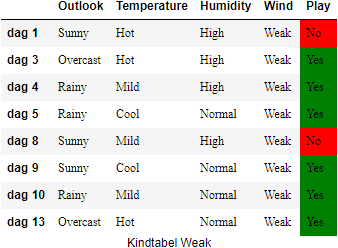
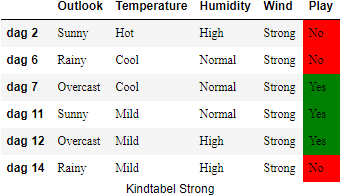
En de bijhorende entropiewaarden zijn:

$E (S_{k i n d, W e a k}) = \sum_{v \in {Y e s, N o}} - \frac{| S_{A = v} |}{| S |} \cdot l o g_{2} \frac{| S_{A = v} |}{| S |}$

$= - \frac{6}{8} \cdot l o g_{2} \frac{6}{8} - \frac{2}{8} \cdot l o g_{2} \frac{2}{8}$

$= 0.811$

$E (S_{k i n d, S t r o n g}) = \sum_{v \in {Y e s, N o}} - \frac{| S_{A = v} |}{| S |} \cdot l o g_{2} \frac{| S_{A = v} |}{| S |}$

$= - \frac{3}{6} \cdot l o g_{2} \frac{3}{6} - \frac{3}{6} \cdot l o g_{2} \frac{3}{6}$

$= 1$

$I G (W i n d) = E (S_{o u d e r}) - \sum_{v \in {W e a k, S t r o n g}} \frac{| S_{k i n d, v} |}{| S_{o u d e r} |} \cdot E (S_{k i n d, v})$

$= E (S_{o u d e r}) - \frac{8}{14} \cdot E (S_{k i n d, W e a k}) - \frac{6}{14} \cdot E (S_{k i n d, S t r o n g})$

$= 0.940 - \frac{8}{14} \cdot 0.811 - \frac{6}{14} \cdot 1$

$= 0.048$

De information gain van $W i n d$ blijft ook lager dan die van $O u t l o o k$ .

Resultaten van stap 1#

We hebben nu alle informations gains voor alle attributen berekend:

	IG
Outlook	0.246750
Temperature	0.029223
Humidity	0.151836
Wind	0.048127

Hieruit blijkt dat we dus best eerst splitsen op het attribuut $O u t l o o k$ , want deze heeft de hoogte IG. In de volgende paragraaf werken we stap 2 van het ID3-algoritme verder uit waarin we deze splitsing doen.

Stap 2#

Uit stap 1 hebben we geleerd dat het splitsen op attribuut $O u t l o o k$ de meest informatiewinst oplevert. Nu pas kunnen een (eerste) node toevoegen aan onze beslissingsboom: een node gelabeled ‘ $O u t l o o k$ ’ met drie uitgaande pijlen voor elk van de waarde die dat attribuut kan aannemen: $S u n n y$ , $O v e r c a s t$ en $R a i n y$ . Dit zijn stappen 2a en 2c uit het ID3-algoritme.

In stap 2c wordt de originele tabel uiteengehaald en opgesplitst in de drie bijhorende kindtabellen: eentje met allemaal de waarde $S u n n y$ , met allemaal de waarde $O v e r c a s t$ , en met allemaal $R a i n y$ in die we reeds gebruikt hebben voor de berekening van $I G (O u t l o o k)$ in stap 1. Het resultaat van stappen 2a t.e.m. 2c worden schematisch weergegeven in onderstaande figuur.

Dit is het moment waarop we stap 2d uit het algoritme op pagina gaan uitvoeren. We bekijken nu de kindtabellen die in bovenstaande figuur nog.

We beginnen links in de figuur met de kindtabel $S_{k i n d, O v e r c a s t}$ . Hiervoor hoeven we het ID3-algoritme niet recursief aangeroepen, want dit is reeds een volledig zuivere tabel met overal $P l a y = Y e s$ . We kunnen deze kindtabel niet verder op te splitsen, want ze bevat allemaal maar $Y e s$ . Dit vormt dan ook een eerst bladnode van onze beslissingsboom in wording.

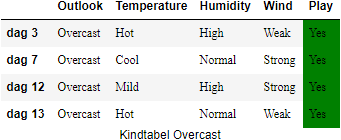
Voor de overige twee kindtabellen, $S_{k i n d, S u n n y}$ en $S_{k i n d, R a i n y}$ moeten we het ID3-algoritme wel recursief gaan toepassen. Merk op dat beide kindtabellen nu gaan optreden als oudertabel.

Opnieuw zullen er dus heel wat information gains berekend moeten worden. Als je alle berekening uitvoert zal je voor de kindtabel $S_{k i n d, S u n n y}$ vinden dat $H u m i d i t y$ de hoogste information gain heeft en dat we daar dus moeten op splitsen.

Voor kindtabel $S_{k i n d, r a i n y}$ zal dan weer $W i n d$ geselecteerd worden.

Alle overgebleven kindtabellen (vier in totaal, twee onder $H u m i d i t y$ en nog eens twee onder $T e m p e r a t u r e$ ) zijn echter volledig zuiver en daarom stopt het ID3 algoritme. De oplossing is gevonden, eindelijk.

Tekortkomingen en oplossingen#

Het ID3-algoritme heeft enkele tekortkomingen, waarvan sommige eerder al vermeld werden, die maken dat de toepasbaarheid ervan beperkter is dan ze op het eerste zicht lijkt. Hier is een overzicht van enkele tekortkomingen of gevaren:

ID3 werkt enkel met discrete, kwalitatieve (nominaal of ordinaal) gegevens: indien je gegevensset toch kwantitatieve (interval of ratio) attributen bevat, moeten deze eerst gediscretiseerd worden in categorieën. Bijvoorbeeld: stel dat het attribuut ‘Temperature’ niet de ordinale waarden ‘Cool’, ‘Mild’, ‘Hot’ had gehad, maar gewoon temperaturen in graden Celsius. Op basis van welke criteria ga je dan categorieën maken? Hoeveel categorieën ga je maken? Hier zijn technieken voor maar die zullen we hier niet behandelen.
ID3 kan niet omgaan met ontbrekende waarden (NA’s): de enige oplossing bestaat erin deze rijen te verwijderen tijdens de data management stap van je proces of om de ontbrekende waarden te vervangen door redelijke alternatieve waarden zoals het gemiddelde, de median, of de meest voorkomende waarde in het geval van kwantitieve gegevens of nog beter door de meest waarschijnlijke waarde gegeven de andere niet-onbrekende waarden (Engels: value imputing). Toch blijven dit allemaal lapmiddeltjes.
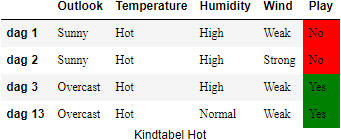
ID3 van pagina kan niet omgaan met inconsistenties in de gegevens: stel dat onze dataset twee of meer rijen heeft waarin alle attributen exact dezelfde waarde hebben, behalve voor target attribuut ‘Play’ zoals de Tabel 2 hieronder. Het probleem met de onderstaande gegevens is dat er geen beslissingsboom van gemaakt kan worden volgens ons beschreven ID3-algoritme.
ID3 heeft (zoals veel andere algoritmes) geen verweer tegen overfitting: ook wanneer je een consistente trainingset hebt, kunnen er toch nog problemen optreden. Het probleem ontstaat omwille van de stopconditie die bepaalt dat het ID3-algoritme de gegevens blijft splitsen tot de subtabellen helemaal zuiver zijn. Voor een consistente trainingset zal dit ook altijd lukken. Dit zorgt ervoor dat de beslissingsboom erg diep kan worden, hetgeen een meestal een teken is dat hij te sterk geconditioneerd is op de instanties uit de trainingset. De beslissingsboom is als het ware een soort van ‘custom-made’ oplossing voor instanties uit de trainingset. Wanneer we de beslissingsboom zouden toepassen op onbekende instanties die niet in de trainingset zitten, zou de resultaten van de voorspelling daarom wel eens heel slecht kunnen zijn!
Information gain heeft een voorkeur (Engels: bias) voor attributen met veel waarden: om dit te begrijpen kan je best een kijkje nemen naar onderstaande trainingset:

Datum

Outlook

Temperature

Humidity

Wind

Play

01/01/2018

Sunny

Hot

High

Weak

No

02/01/2018

Sunny

Hot

High

String

No

03/01/2018

Overcast

Hot

High

Weak

Yes

…

…

Tabel: Probleem met entropie

Information gain zal het attribuut ‘Datum’ selecteren als het meest informatieve attribuut omdat het alle instanties meteen correct classificieert. Het probleem hiermee is dat er beslissingsboom ontstaat met een root node ‘Datum’ met daaronder voor elke datum een tak die eindigt in een bladnode met exacte één instantie in, nl.: de instantie die hoort bij die datum. Hoewel deze beslissingsboom alle instanties uit de trainingset perfect kan classificeren, is deze beslissingsboom waardeloos bij het voorspellen van nieuwe, onbekende dagen (want er bestaat helemaal geen tak voor)!

Datum	Outlook	Temperature	Humidity	Wind	Play
01/01/2018	Sunny	Hot	High	Weak	No
02/01/2018	Sunny	Hot	High	String	No
03/01/2018	Overcast	Hot	High	Weak	Yes
…					…

Oplossingen

Voor elk van deze problemen bestaat er een oplossing. Sommige problemen worden opgelost m.b.v. een nieuwere en beter versie van het ID3-algoritme dat bekend geworden is onder de naam C4.5 (en in sommige softwaretools wordt het ook J48 genoemd). We sommen de oplossingen hieronder op:

Het C4.5 algoritme kan wel overweg met continue, en kwantitatieve gegevens door m.b.v. statistische technieken (die we hier niet behandelen) goede drempelwaarden te bereken die gebruikt kunnen worden in logische testen op attribuutwaarden. Zo kunnen nodes in C4.5 beslissingsboom takken hebben met vergelijkingsoperatoren (<, >) om te bepalen of een instantie al dan niet in die tak thuishoort.
Ook voor ontbrekende waarden heeft het C4.5 algoritme een oplossing, die bestaat uit twee delen:
- elk attribuut van elke instantie krijgt een gewicht dat normaal gesproken gelijk is aan ‘1’.
- bij een instantie met een ontbrekende waarde voor een attribuut A, maakt het algoritme een v-tal kopieën aan van deze instantie en vervangt in elke kopie de waarde van het ontbrekende attribuut door één van de mogelijke waarde v die het attribuut kan aannemen. De gewichten van die attributen worden aangepast naar de kans dat de waarde v voorkomt in de subtabellen die ontstaan op dat punt in beslissingsboom. Bij de berekening van entropie en information gain wordt rekening gehouden met het gewicht van het attribuut.
Het ID3 algoritme zoals beschreven op pagina kan niet omgaan met inconsitente gegevens maar dit kan op zich makkelijk opgelost worden. Voor alle inconsistente instanties kan er gekeken worden naar de meest voorkomende target attribuut value, zodat deze gebruikt wordt. Indien alle uitkomsten evenveel voorkomen, kan een willekeurige keuze gemaakt worden. In software pakketten zit deze functionaliteit wel ingebouwd in het ID3 en C4.5 algoritme.
Er bestaat een algemene techniek, genaamd cross-validatie die gebruikt kan worden om overfitting tegen te gaan: je houdt een deel van je trainingset apart onder de naam validatieset. Voor beslissingsbomen kan je deze techniek nu weer op twee manieren inzetten:
- pre-pruning: tijdens het bouwen van je beslissingsboom test je de kwaliteit van je beslissingboom op je validatie-test. Zolang die blijft verbeteren, kan je doorgaan met het verfijnen en uitbreiden van je beslissingsboom anders stop je.
- post-pruning: je bouwt eerst een belissingsboom met een maximale diepte. Vervolgens knip je takken weg en test de performantie van de geknipte beslissingsboom op je validatieset. Blijf knippen zolang de kwaliteit van je oplossing goed blijft werken op de validatieset. Je zal een algemenere oplossing overhouden.
Gain Ratio en Gini zijn verbeterde versies van Information Gain die een splitsing in zeer veel takken bestraffen waardoor betere keuzes gemaakt worden qua attribuutselectie.

ID3 in Python#

Eigen implementatie#

Het is relatief eenvoudig om het ID3 - algoritme te programmeren in Python omdat Python een zeer goede ondersteuning biedt voor data management operaties en manipulaties. We tonen hier alvast de functie om de entropy van een Pandas Series te berekenen, en een functie om de information gain te berekenen:

import numpy as np
import pandas as pd

def entropy(series: pd.Series, base=None):
    # bepaal de verhoudingen
    vc = series.value_counts(normalize=True, sort=False)
    base = 2 if base is None else base
    # gebruik Numpy broadcasting principe
    return -(vc * np.log(vc) / np.log(base)).sum()


def information_gain(parent_table: pd.DataFrame, attribute: str, target: str):
    # bepaal entropie van parent table
    entropy_parent = entropy(parent_table[target])
    child_entropies = []
    child_weights = []

    # bereken entropies of child tables
    for (label, fraction) in parent_table[attribute].value_counts().items():
        child_df = parent_table[parent_table[attribute] == label]
        child_entropies.append(entropy(child_df[target]))
        child_weights.append(int(fraction))

    # bereken het verschil tussen ouder entropie and gewogen kind entropieën.
    return entropy_parent - np.average(child_entropies, weights=child_weights)

We laten het effectief implementeren van het recursieve ID3 algoritme over als een oefening.

Bestaande implementaties#

Voor zowel het ID3 en C4.5 algoritme bestaan er reeds meerdere implementaties van de algoritmes. Omdat het ID3 algoritme omwille van de eerdere vernoemde beperkingen een eerder didactische aard heeft gekregen in loop der jaren wordt het veel minder gebruikt. Zo komt het dat de Scikit Learn library er geen implementatie van aanbiedt. Daarom gebruiken we voor ID3 de Id3Estimator implementatie.

ID3#

Eerst moeten we Id3Estimator installeren. Er zijn enkele bugs in dit algoritme omdat het niet actief onderhouden wordt. Zo heeft het enkele dependencies op de Scikit Learn library die stuk zijn. Daarom moet je Scikit Learn momenteel (mei 2021) downgraden naar versie 0.22.

pip install sklearn==0.22     # downgrade Scikit Learn
pip install decision-tree-id3 # install Id3Estimator

Met een kleine hack kan je het nu als volgt gebruiken, en dan nog zal je enkele warnings krijgen die je mag verwaarlozen.

import graphviz
import pandas as pd
import six
import sys

# hack om Id3Estimator tevreden te stellen
from id3.export import DotTree
sys.modules['sklearn.externals.six'] = six
from id3 import Id3Estimator, export_graphviz

weather_nominal = pd.read_csv('datasets/weather_nominal.csv', dtype='category')

attributen = weather_nominal.drop(columns=['Play'])
target = weather_nominal.Play

# X en y MOETEN gewone Python lists zijn, anders werkt het niet.
X = attributen.to_numpy().tolist()
y = target.to_numpy().tolist()

# model bouwen en fitten op trainingsgegevens
model = Id3Estimator()
model.fit(X, y)

# beslissingsboom visualiseren.
model_tree = DotTree()
export_graphviz(model.tree_,model_tree,feature_names=attributen.columns)
graphviz.Source(model_tree.dot_tree)

We kunnen nu uiteraard ook voorspellingen doen met dit model.

dag15en16 = [
    ['Overcast','Hot','Normal','Weak'],
    ['Rainy','Cool','High','Strong']
]
model.predict(dag15en16)

array(['Yes', 'No'], dtype='<U3')

C4.5#

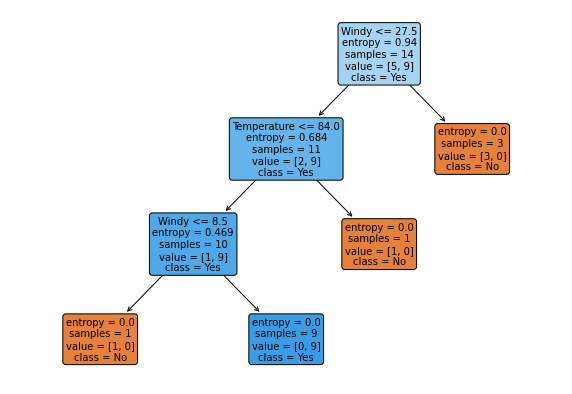
Scikit Learn biedt veel machine learning algoritmen aan, en dus ook een implementatie van C4.5, genaamd, DecisionTreeClassifier. Deze implementatie werkt echter niet met nominale of ordinale variabelen, en we kunnen het dan ook niet rechstreeks toepassen op de nominale dataset van hierboven. Daarom gebruiken we nu een andere dataset die enkele gegevens op de ratiomeetschaal bevat voor de attributen.

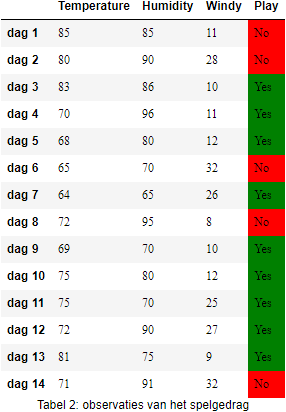
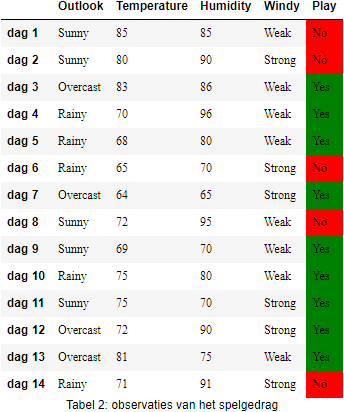
Op deze tabel kunnen we DecisionTreeClassifier loslaten. We verwijzen naar de documentatie voor alle mogelijkheden, maar hieronder zie je alvast een voorbeeld toegepast op de Tabel 2.

import numpy as np
from sklearn import tree
from sklearn.tree import DecisionTreeClassifier

model = DecisionTreeClassifier(criterion='entropy')
X = weather_ratio.drop(columns=['Play'])
y = weather_ratio.Play
model.fit(X, y)

tree.plot_tree(model,
               feature_names=X.columns,
               class_names=np.unique(y),
               filled=True, fontsize=12, rounded=True)

DecisionTreeClassifier(ccp_alpha=0.0, class_weight=None, criterion='entropy',
                       max_depth=None, max_features=None, max_leaf_nodes=None,
                       min_impurity_decrease=0.0, min_impurity_split=None,
                       min_samples_leaf=1, min_samples_split=2,
                       min_weight_fraction_leaf=0.0, presort='deprecated',
                       random_state=None, splitter='best')

We kunnen ons tot slot afvragen hoe we een beslissingsboom kunnen bouwen voor datasets waarin alle meetschalen voorkomen. Dit is ook mogelijk mits we de nominale en ordinale gegevens coderen. Gelukkig bieden zowel Pandas als Scikit Learn hier mogelijkheden voor. We bekijken hoe Pandas ons kan helpen.

We kunnen de attributen omzetten met de Pandas functie pd.get_dummies zodat de nominale en ordinale variabele gecodeerd worden.

import pandas as pd

pd.get_dummies(weather.drop(columns=['Play']))

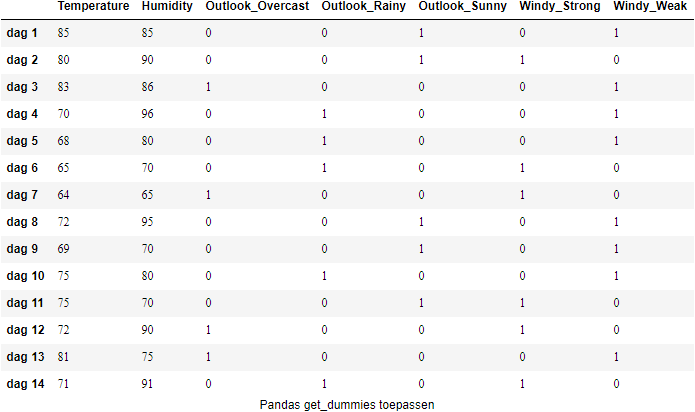
Pandas get_dummies zet $O u t l o o k$ en $W i n d y$ om naar respectievelijk 3 en 2 extra kolommen, maar behoudt $T e m p e r a t u r e$ en $H u m i d i t y$ zoals het hoort. Per waarde die een nominale of ordinale kolom kan aannemen wordt een extra kolommen gemaakt. Voor $O u t l o o k$ zijn dat dus de kolommen $O u t l o o k_O v e r c a s t$ , $O u t l o o k_R a i n y$ en $O u t l o o k_S u n n y$ .

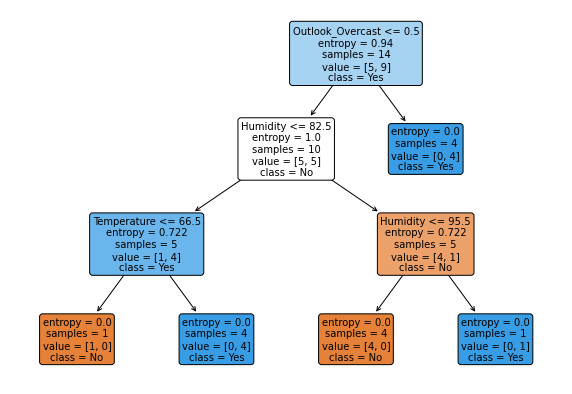
We kunnen deze nieuwe attributen nu gebruiken als input voor het model.

model = DecisionTreeClassifier(criterion='entropy')
X = pd.get_dummies(weather.drop(columns=['Play']))
y = weather.Play

model.fit(X, y)

_ = tree.plot_tree(model,
                   feature_names=X.columns,
                   class_names=np.unique(y),
                   filled=True, fontsize=10, rounded=True)

met als resultaat deze beslissingsboom.

DecisionTreeClassifier(ccp_alpha=0.0, class_weight=None, criterion='entropy',
                       max_depth=None, max_features=None, max_leaf_nodes=None,
                       min_impurity_decrease=0.0, min_impurity_split=None,
                       min_samples_leaf=1, min_samples_split=2,
                       min_weight_fraction_leaf=0.0, presort='deprecated',
                       random_state=None, splitter='best')

Ensembles#

Alle machine learning technieken die meerdere modellen combineren worden ensembles genoemd. Een ensemble lijkt een beetje op een jury of een commissie die een beslissing moet nemen. Alle leden van de jury noteren hun beslissing en de meerderheidsstem wint.

Waarom zouden we onze beslissing dus overlaten aan één beslissingsboom als we er ook meerdere kunnen gebruiken?

Deze techniek staat bekend als Random Forest en Gradient Boosted Trees. Ze leveren meestal zéér goede resultaten, vergelijkbaar met neurale netwerken, maar met het voordeel dat ze door een mens kunnen geïnterpreteerd worden. Deze technieken worden gebruikt op grote datasets, en de verschillende bomen komen tot stand doordat er telkens op random wijze een nieuwe trainingsset gesampled wordt van de originele dataset. Omdat elke trainingsset anders opgebouwd is, krijgen we telkens ook een andere beslissingsboom.

Met Scikit Learn kan je deze ensembles maken. Hier is een voorbeeld van de Scikit Learn website ter illustratie.

from sklearn.datasets import make_hastie_10_2
from sklearn.ensemble import GradientBoostingClassifier

X, y = make_hastie_10_2(random_state=0)
X_train, X_test = X[:2000], X[2000:]
y_train, y_test = y[:2000], y[2000:]

model = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
                                    max_depth=1, random_state=0)

model.fit(X_train, y_train)
model.score(X_test, y_test)

Er worden 100 beslissingsbomen gebouwd die wel allemaal gelimiteerd worden tot een diepte van slechts 1 niveau, toch levert dit een nauwkeurigheid van 93%.

Referenties#

BFSO84: Leo Breiman, Jerome Friedman, Charles J Stone, and Richard A Olshen. Classification and regression trees. CRC press, 1984.
Qui86: J. Ross Quinlan. Induction of decision trees. Machine learning, 1(1):81–106, 1986.
Sal94: Steven L Salzberg. C4. 5: programs for machine learning by j. ross quinlan. morgan kaufmann publishers, inc., 1993. 1994.

Data Science 1

Beslissingsbomen

Contents