Spreidingsmaten#

Bekijk volgende data:

import pandas as pd

x1 = pd.Series([1, 2, 3, 5, 87, 88, 89, 90])
x2 = pd.Series([42, 43, 44, 45, 47, 47, 48, 49])

Als we het gemiddelde van deze reeksen berekenen, dan vinden we bij beiden $45.625$ . Ook de mediaan is dezelfde: $46$ :

pd.DataFrame([[x1.mean(), x2.mean()],
              [x1.median(), x2.median()]],
             index=['mean()', 'median()'], columns=['x1', 'x2'])

	x1	x2
mean()	45.625	45.625
median()	46.000	46.000

Toch is er een heel groot verschil tussen deze twee reeksen. De waarden in x1 schommelen veel harder rond het centrum dan de waarden in x2. Men zegt dat de spreiding van de waarden in x1 groter is dan die van x2.

Er zijn verschillende manieren om de spreiding te bepalen. We bespreken er hier drie:

bereik,
interkwartielafstand en
standaardafwijking.

Bereik#

De eenvoudigste manier om de spreiding van waarden te bepalen, is door te kijken naar het bereik. Dit is het verschil tussen de maximale en de minimale waarde. Het bereik kan je dus pas bepalen vanaf intervalmeetniveau.

In het bovenstaande voorbeeld levert dit:

x1.max() - x1.min()

x2.max() - x2.min()

Het bereik is dus gemakkelijk te bepalen, maar er is een groot nadeel: het bereik wordt heel sterk beïnvloed door uitschieters. Stel dat er bijvoorbeeld een hele hoge of een hele lage waarden tussen zit, dan zal het bereik sterk veranderen, enkel en alleen omdat er 1 verkeerde waarde tussen zit.

Interkwartielafstand#

We kunnen het idee van de mediaan veralgemenen. Bij de mediaan sorteren we alle gegevens en nemen de middelste waarde. Dat betekent dat 50% van de gegevens kleiner is dan de mediaan en 50% groter.

We kunnen de gesorteerde lijst ook in meer delen splitsen. Dikwijls splitst men deze lijst in 4 gelijke delen. De waarden op de grenzen (dit zijn er 3, geen 4!), noemt men de kwartielen. Men nummert deze Q1, Q2 en Q3. Ze splitsen de data dus in 4 delen die elk 25% van de gegevens bevatten. In Python kan je deze kwartielen als volgt berekenen:

laptops.diskspace.quantile(q=[0.25, 0.5, 0.75])

0.25    227.80
0.50    249.80
0.75    489.85
Name: diskspace, dtype: float64

De kwartielen staan respectievelijk bij 25%, 50% en 75%. Bemerk dat het tweede kwartiel (Q2) gelijk is aan de mediaan!

Je kan ook in meerdere delen splitsen. Men spreekt dan van decielen (in 10 delen), percentielen (100 delen) of kwantielen (algemene naam). Zo is 30 procent van alle getallen lager dan het derde deciel of het dertigste percentiel. Aangezien er in de praktijk vooral met kwartielen wordt gewerkt, zullen we daar ook meer nadruk op leggen.

We willen nu de spreiding van de gegevens weergeven zonder rekening te houden met extreem lage of extreem hoge waarden. Die waarden zitten in de eerste 25% of de laatste 25%. Daarom dat we deze weg laten en dan kijken wat het bereik is. Dat noemt men de interkwartielafstand. Je bepaalt die dus door Q3-Q1 te berekenen.

In Python kan je dit als volgt berekenen:

from scipy import stats

stats.iqr(laptops.diskspace.dropna())

262.05

Dit geeft dus het bereik van de data wanneer je de 25% laagste waarden en de 25% hoogste waarden verwijdert.

De interkwartielafstand is een maat voor de spreiding van de gegevens rond de mediaan. Ze wordt dus ook altijd in combinatie met de mediaan gebruikt. Let wel op: de interkwartielafstand kan je enkel berekenen vanaf interval meetniveau (want je trekt 2 waarden van elkaar af), terwijl de mediaan en de kwartielen al bestaan vanaf ordinaal meetniveau.

Er bestaat een grafiek die heel duidelijk de kwartielen en het bereik weergeeft: de boxplot. De grafiek toont een rechthoek (“box”) met een streep in. De streep geeft aan waar de mediaan zit en de boven- en onderkant geven aan waar het eerste en het derde kwartiel zitten. Meestal duidt men ook het maximum en het minimum aan en uitschieters (zie verder) worden door bolletjes weergegeven.

Je kan in Python een boxplot genereren met (gebruik dit wel binnen een figure):

from matplotlib import pyplot as plt

fig, ax = plt.subplots()
ax.boxplot(laptops.diskspace.dropna())
ax.set_title('Schijfruimte in laptops')
_ = ax.set_ylabel('Schrijfruimte(GB)')

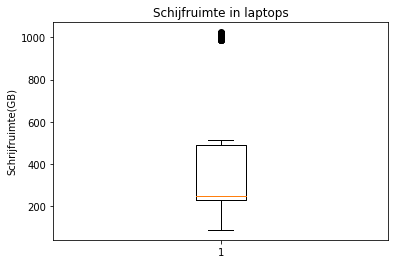
Je ziet dat Python hierbij een aantal uitschieters vindt (de donkere, dikke lijn bovenaan, die eigenlijk bestaat uit een aantal punten, dicht bij elkaar). Meer daarover in sectie Uitschieters.

Standaardafwijking#

De interkwartielafstand is een heel goede maat voor de spreiding van gegevens, maar er is (net zoals bij de mediaan) geen exacte formule om deze uit te rekenen. Dat maakt het moeilijk om op een wiskundige manier eigenschappen te vinden die nuttig zijn bij analyses.

Daarom dat er nog een andere manier is om de spreiding te bepalen. Deze spreiding is verwant aan het gemiddelde. We zoeken dus hoe sterk de waarden variëren rond het gemiddelde.

Dit gebeurt door te kijken naar het verschil tussen de waarden en het gemiddelde. Als deze verschillen allemaal klein zijn, schommelen de waarden dus niet veel rond het gemiddelde en is er sprake van een kleine spreiding. Het is niet praktisch om te kijken naar alle verschillen tussen de waarden en het gemiddelde.

Daarom dat men het gemiddelde neemt van al deze verschillen. In Python ziet dit er als volgt uit:

x = laptops.diskspace.dropna()
verschillen = x - x.mean()
verschillen.mean()

-4.849391550287499e-14

Het resultaat is heel erg klein, waardoor je zou kunnen denken dat de spreiding dus ook heel klein is. Er is echter een foutje in bovenstaande redenering: de verschillen tussen de waarden en het gemiddelde zijn niet altijd positief. Soms zijn ze ook negatief en daardoor is het resultaat altijd 0 (door afrondingsfouten en cancellation met floating-point getallen vinden we niet altijd exact 0).

Een oplossing bestaat erin om de verschillen allemaal positief te maken. Dat kan op 2 manieren: je neemt de absolute waarde of je kwadrateert ze. Als we de absolute waarde nemen, krijg je het volgende:

verschillen = (x - x.mean()).abs()
verschillen.mean()

163.32447262569372

De functie mad() doet dit ineens:

x.mad()

163.32447262569372

Wiskundig is de formule:

M A D_{x} = \frac{1}{n} \sum_{i = 1}^{n} | x_{i} - \overset{―}{x} |

De waarden schommelen dus gemiddeld $163.3245$ rond het gemiddelde. Deze waarde noemt men de “mean absolute deviation” (MAD). Je kan het gemiddelde in deze formule ook vervangen door de mediaan en dan vind je de “median absolute deviation” (ook afgekort als MAD). Het nadeel is echter dat deze formule nog steeds niet goed wiskundig bruikbaar is omdat de absolute waarde niet afleidbaar is. Dat gaat wel als we kwadraten gebruiken. Een kwadraat van een getal is namelijk ook altijd positief.

Als we met kwadraten werken, trekken we op het einde terug de wortel uit het getal:

import math

verschillen = (x - x.mean()) ** 2
math.sqrt(verschillen.mean())

199.07084050739573

Wiskundig ziet dit er als volgt uit:

s_{x} = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} (x_{i} - \overset{―}{x})^{2}}

Dit noemt men de “standaardafwijking”. We zullen de standaardafwijking van een variabele $x$ weergeven met het symbool $s_{x}$ . De formule om deze te bepalen is gemakkelijk te gebruiken om allerlei eigenschappen aan te tonen en te bewijzen.

Het kwadraat van de standaardafwijking heeft ook een naam: “variantie”. Dit kom je ook regelmatig tegen in de literatuur.

In Python is er een functie die direct de standaardafwijking berekent:

x.std()

199.18790658073468

Zoals je ziet, geeft deze een (licht) ander resultaat. Dat komt omdat we meestal proberen om de standaardafwijking van de populatie te vinden. De standaardafwijking die we hiervoor definieerden, zou deze moeten benaderen als de steekproef groot genoeg is. Maar als de steekproef kleiner is, dan kan men aantonen dat we de standaardafwijking onderschatten. Daarom dat er een kleine compensatie gebeurt en men in de praktijk altijd volgende formule gebruikt. Men noemt dit ook de Bessel correctie:

s_{x} = \sqrt{\frac{1}{n - 1} \sum_{i = 1}^{n} (x_{i} - \overset{―}{x})^{2}}

In Python kan je dit ook vinden met:

n = len(x)
verschillen = (x - x.mean()) ** 2
math.sqrt(verschillen.mean() * n / (n - 1))

199.18790658073468

We vinden nu hetzelfde resultaat, maar de functie std() is natuurlijk veel eenvoudiger.

Uitschieters#

Er is in bovenstaande tekst al regelmatig verwezen naar uitschieters. Uitschieters zijn extreem lage of extreem hoge waarden. Ze worden ook outliers of extremen genoemd. Ze kunnen door verschillende oorzaken ontstaan:

mensen kunnen per ongeluk een 0 te veel of te weinig hebben getypt
er werd doelbewust verkeerde data ingegeven. Niet iedereen is even enthousiast om een vragenlijst in te vullen…
in een meting kan er af en toe een fout gebeuren (bv: CO2 meters geven af en toe onrealistische waarden omdat er heel tijdelijk meer of minder CO2 in de detector komt)
soms zijn er mogelijke waarden die heel hoog of heel laag zijn, maar komen ze heel weinig voor. We willen deze dan verwijderen omdat ze te veel invloed geven op het besluit

Uitschieters hebben veel invloed op het gemiddelde en de standaardafwijking, maar niet op de mediaan en de interkwartielafstand.

We kunnen dit duidelijk maken aan de hand van een voorbeeld. Stel dat we met opzet een foute meting in de dataset aanbrengen en dan kijken naar het verschil.

We kijken eerst naar de data (zonder de foute meting), zoals ze zou moeten zijn:

x = laptops.RAM
x.mean()

6.130994152046783

x.std()

4.662789148190274

x.median()

4.0

stats.iqr(x.dropna())

4.0

We voegen nu een foute meting in. In dit geval dacht iemand dat het RAM-geheugen in MB moest worden opgegeven. Daardoor komt er ineens een hele grote waarde in de tabel. We voegen deze uitschieter toe en berekenen alle waarden opnieuw:

x.at[42] = 8192 # foute meting invoegen
x.mean()

15.702923976608187

x.std()

279.98970904200445

x.median()

4.0

stats.iqr(x.dropna())

6.0

fig, ax = plt.subplots()
ax.boxplot(x.dropna())
ax.set_title('RAM in laptops')
_ = ax.set_ylabel('RAM(GB)')

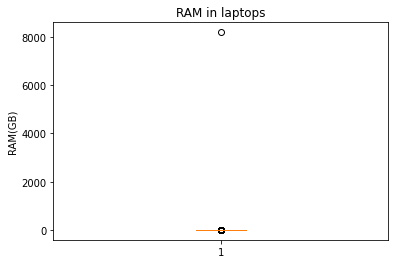
Je ziet dat het gemiddelde en de standaardafwijking sterk veranderen, maar de mediaan en de interkwartielafstand blijven gelijk. Daarom dat de laatste twee een heel goede keuze zijn om centrum en spreiding te bepalen. De boxplot toont ook heel duidelijk dat er na onze aanpassing iets niet in de haak zit.

Maar soms moet je wel degelijk het gemiddelde en de standaardafwijking gebruiken en wil je de uitschieters eerst verwijderen. De vraag is dus of we uitschieters kunnen identificeren.

Er zijn een aantal methoden om dit te doen, maar de meest gebruikte, werkt als volgt:

bepaal de 3 kwartielen: Q1, Q2 en Q3 en de interkwartielafstand IQR
bereken nu:
- $l = Q 1 - 1, 5 \cdot I Q R$
- $h = Q 3 + 1, 5 \cdot I Q R$
alle waarden die kleiner zijn dan $l$ of hoger dan $h$ , noemen we uitschieters.

Deze manier wordt in heel wat softwarepakketten gebruikt. Soms spreekt met ook van “extreme uitschieters”. Die bepaal je door de factor 1,5 te vervangen door 3 in de bovenstaande formules.

In Python kunnen we een functie schrijven die uitschieters kan bepalen:

def outlier_boundaries(x, factor=1.5):
    Q1 = x.quantile(0.25)
    Q3 = x.quantile(0.75)
    I = Q3 - Q1
    return [Q1 - factor * I, Q3 + factor * I]

Als we deze gebruiken op de data van hiervoor, dan krijgen we:

low, high = outlier_boundaries(x)
pd.DataFrame([low, high], index=['low', 'high'], columns=['outlier grenzen'])

	outlier grenzen
low	-2.0
high	14.0

Je ziet dat zelfs laptops met 16 GB hier als een uitschieter zouden worden bekeken. Dat komt omdat de schaal niet lineair is: 1, 2, 4 en 8 liggen redelijk dicht bij elkaar en 16 ligt daar relatief ver van af. Het is dus altijd belangrijk om na te gaan of de uitschieters effectief uitschieters zijn! In dit geval zouden we 16 beter niet als uitschieter beschouwen, maar de 8192 wel.

Als de gegevens wel lineair zijn, zullen de waarden van $l$ en $r$ meestal wel goed aangeven waar de uitschieters te vinden zijn, maar je verifieert dit best handmatig.

Als je uitschieters wil verwijderen, kan dat bijvoorbeeld als volgt doen met de between()-methode.

x = x[x.between(low, 16)]

fig, ax = plt.subplots()
ax.boxplot(x.dropna())
ax.set_title('RAM in laptops')
_ = ax.set_ylabel('RAM(GB)')

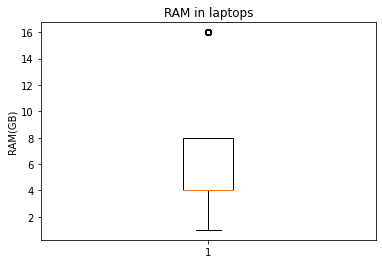
Warning

Merk op dat de boxplot() functie 16 GB nog steeds als een uitschieter beschouwt. Dat komt omdat ze ook dezelfde definties voor uitschieters gebruikt. De originele grenzen zaten tussen $- 2$ en $14$ , maar wij hebben de bovengrens toch verzet naar 16 GB in bovenstaand stukje code.

Data Science 1

Spreidingsmaten

Contents