Afstanden meten#

In de volgende paragrafen zullen we toelichten hoe we het begrip afstand kunnen definiëren voor gegevens met meerdere dimensies. We beginnen eenvoudig met een-dimensionale gegevens en breiden dit verder uit naar hogere dimensies. We zullen ontdekken dat er verschillende manieren zijn om de afstand te meten tussen twee instanties van onze datasets. De belangrijkste afstandsmaat wordt de Euclidische afstandsmaat genoemd omdat deze gebaseerd is op de Stelling van Pythagoras uit de Euclidische meetkunde.

Eén-dimensionele gegevens#

We hebben dataset met daarin de examenscores van 327 eerstejaarsstudenten. Hieronder zie je enkel scores voor het examen Data Science 1.

We hebben deze examenscores ook geplot op een 1D-lijngrafiek, en omdat sommige studenten natuurlijk hetzelfde cijfer behaalden, kan je niet goed zien dat het hier effectief om 327 studenten gaat. Daarom hebben we voor de duidelijkheid een tweede 1D-lijngrafiek gemaakt waarop de examenscores verticaal een beetje verpreid zijn (jitter toepassen) zodat ze duidelijker wordt dat het hier om zoveel meetpunten gaat. We hebben ook de afstanden tussen de studenten 1, 2 en 327 aangeduid met pijltjes.

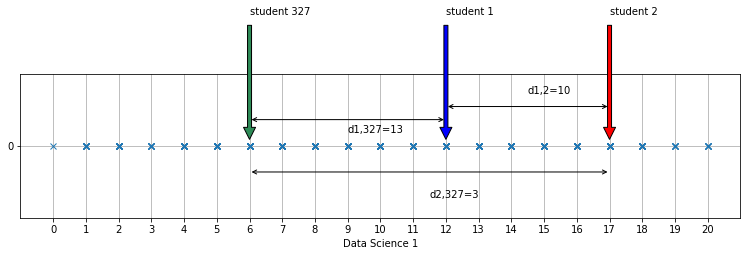
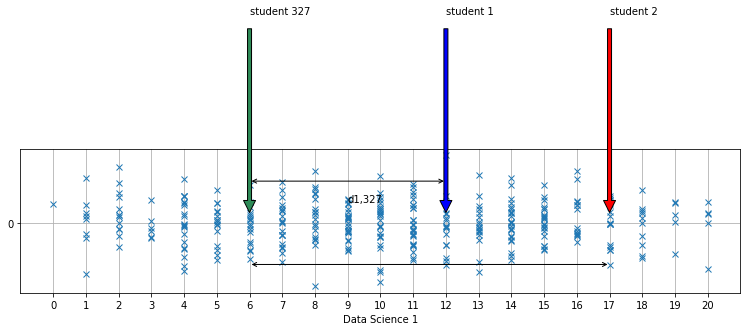
We kunnen nu heel makkelijk uitspraken doen over de scores van studenten door het verschil te berekenen van de scores van twee studenten uit deze dataset, want de scores zijn namelijk gemeten op een ratio meetniveau.

Voorbeeld: student 1 behaalde een 15 op 20 en student 2 een 5 op 20. De afstand $d_{1, 2}$ tussen deze twee studenten bedraagt:

d_{1, 2} = | 15 - 5 | = 10

Voorbeeld: student 1 behaalde een 15 op 20 en student 327 een 2 op 20. De afstand $d_{1, 327}$ tussen deze twee studenten bedraagt:

d_{1, 327} = | 15 - 2 | = 13

Merk op dat we de afstanden $d_{1, 2}$ en $d_{1, 327}$ ook kunnen bepalen met de volgende (meer algemene) berekeningswijze waarvan verderop duidelijk wordt hoe deze bekomen wordt.

d_{1, 2} = \sqrt{(15 - 5)^{2}} = 10

d_{1, 327} = \sqrt{(15 - 2)^{2}} = 13

Met deze afstandsberekeningen kunnen we ons aanvoelen makkelijk quantificeren, namelijk dat student 1 beter scoort dan student 2 en dat student 327 slechter is dan beide vorige studenten en ook hoeveel beter iemand is.

Twee-dimensionele gegevens#

Stel nu dat we ook de examenscores van Programmeren 1 toevoegen aan onze dataset onder een kolom ‘Programmeren 1’

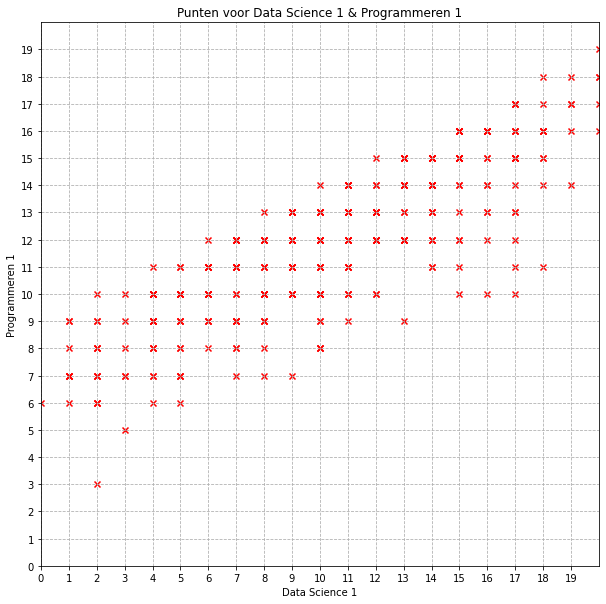
Maar hoe kunnen we nu de afstanden berekenen tussen de verschillende studenten? Dit kunnen we door de Stelling van Pythagoras toe te passen. In Figuur zie je hoe de coördinaten van studenten 1 en 2 een rechthoekige driehoek vormen en in een rechthoekige driehoek geldt de stelling van Pythagoras: $a^{2} + b^{2} = c^{2}$ . Hieruit volgt dat de schuine zijde gelijk is aan $c = \sqrt{a^{2} + b^{2}}$ en wanneer we dit toepassen op de rechthoek uit Figuur krijgen we:

d_{1, 2} = \sqrt{(p_{1} - p_{2})^{2} + (q_{1} - q_{2})^{2}}

waarbij we de onnodig absolute waarde - tekens hebben weggelaten want het kwadraat maakt de verschillen toch ook steeds positief. Om de afstand te berekenen tussen twee instanties van onze dataset moeten we dus gewoon hun scores op Data Science van elkaar aftrekken en kwadrateren en hetzelfde doen voor hun scores op Programmeren 1. Daarna nemen we de wortel van de som de twee gekwadrateerde verschillen. De afstand die we zo bekomen wordt de Euclidische afstand genoemd. Zoals we reeds paragraaf Eén-dimensionele gegevens aangaven, werkt de Euclidische afstandsformule ook met één-dimensionele data.

Het punt p ligt in ons voorbeeld in de oorsprong, maar dit is geen vereiste: de punten p en q mogen eender waar liggen

Drie-dimensionele gegevens#

Uiteraard zijn er nog meer vakken waarvan we de examenscores zouden kunnen in rekening brengen. Laten we daarom Computersystemen 1 ook nog toevoegen aan onze dataset onder alweer een nieuwe kolom ‘Computersystemen 1’.

We kunnen deze gegevens nu plotten als een 3D-puntenwolk

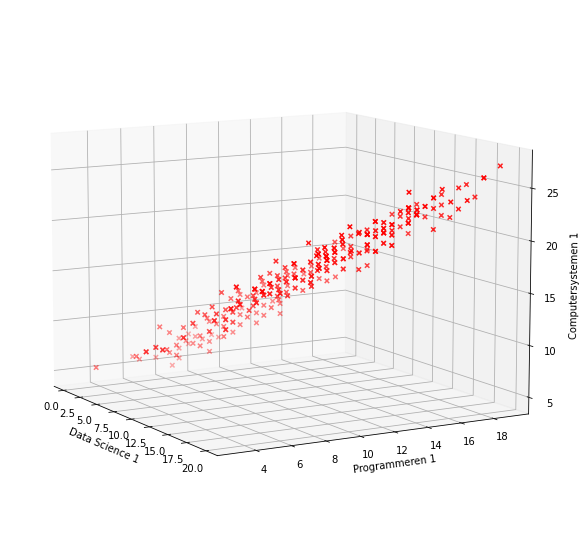
Met behulp van de formule voor de Euclidische afstand uit paragraaf Twee-dimensionele gegevens kunnen we de afstand tussen onze studenten in drie dimensies dan ook eenvoudig berekenen.

Voorbeeld

We bereken de afstanden tussen student 1 en 2, student 1 en student 327 en student 2 en student 327

$d_{1, 2} = \sqrt{(10 - 8)^{2} + (12 - 7)^{2} + (11 - 10)^{2}}$

$= 5.48$

$d_{1, 327} = \sqrt{(10 - 14)^{2} + (12 - 17)^{2} + (11 - 15)^{2}}$

$= 7.55$

$d_{2, 327} = \sqrt{(8 - 14)^{2} + (7 - 17)^{2} + (10 - 15)^{2}}$

$= 12.69$

N-dimensionele gegevens#

We hoeven natuurlijk niet te stoppen bij slechts drie examenresultaten. We kunnen gewoonweg alle examenresultaten opnemen, en indien gewenst kunnen we ook andere gegevens over studenten opnemen zoals hun leeftijd, tijdstip van inschrijving, aantal broers of zussen, … zolang we voor de toegevoegde dimensies maar een afstandscriterium hebben kunnen we de afstand tussen onze instanties in onze dataset berekenen.

We gaan deze redenering nu nog een beetje verder doortrekken. We weten nu dat elk attribuut (Data Science, Programmeren 1, …) uit onze dataset een extra dimensie toevoegt en tot en met drie dimensies kunnen we ons dit zelfs nog voorstellen als punten in een ruimte. We kunnen deze punten ook verbinden door middel van een lijn met de oorsprong van het assenstelsel en op die manier krijgen we zogenaamde vectoren. Elke instantie uit onze dataset wordt een vector in een N-dimensionele ruimte.

Voorbeelden

PNG’s Een PNG-foto van 512 bij 512 pixels waarbij voor elke pixel er 4 kanalen (rood, groen, blauw en transparantie) zijn. Voor elk kanaal zijn er tevens 256 mogelijke waarden. Alle 512 x 512 PNG-foto’s bevinden zich in een 268435456-dimensionele ruimte (512 x 512 x 4 x 256). De foto van Lenna hieronder is slechts één punt (of één vector) in deze ruimte. Als vector kan ze dan ook vergeleken worden m.b.v. de Euclidische afstandsformule met alle andere 512x512 PNG-foto’s die er bestaan in het ons universum.

Teksten

Een verzameling van tekstdocumenten kunnen eveneens voorgesteld worden als punten (en vectoren) in een N-dimensionele ruimte door elk document voor te stellen als een zogenaamde Bag of Words (BOW). Een BOW reduceert een document tot een absolute frequentie tabel van alle woorden die voorkomen in alle documenten, i.e. de gebruikte vocabulaire. Stel dat we drie heel eenvoudige documenten hebben

document 1: “hond hond kat”
document 2: “kat muis hond”
document 3: “kat kat muis paard”

Deze drie documenten kunnen voorgesteld worden in een 4-dimensionele ruimte omdat de vocabulaire uit vier woorden bestaat (hond, kat, muis en paard). Deze vier woorden vormen tevens de vier assen van het assenstelsel. We kunnen de drie documenten nu omzetten naar een dataset waarbij elk document een instantie (een rij) is.

document	hond	kat	muis	paard
1	2	1	0	0
2	1	1	1	0
3	0	2	1	1

Uit de dataset kunnen we nu ook heel makkelijk de coördinaten voor de documenten in dit assenstelsel aflezen:

document 1: (2,1,0,0)
document 2: (1,1,1,0)
document 3: (0,2,1,1)

De BOW-voorstelling van de documenten herleidt deze tot eenvoudige vectoren in een 4-dimensionale ruimte waardoor ze kunnen vergeleken worden met andere documenten. Gelijkaardige technieken worden door zoekmachines toegepast om voor jouw zoekopdrachten de meest gepaste websites af te leveren.

Andere afstandsmaten#

In de vorige paragraaf hebben we al kort aangehaald dat er naast de Euclidische afstand nog heel wat andere afstandsmaten bestaan. We behandelen deze hier kort.

Manhattan afstand: Deze afstandsmaat wordt ook wel de ‘taxi’-afstand genoemd omdat je alleen maar volgens rechthoeken mag afslaan zoals bij het stratenplan van Amerikaanse steden. Je kan deze afstand ook weer in verschillende dimensies gaan uitrekenenen net zoals dat kon bij de Euclidische afstandsmaat, de formule is nu gelijk aan:

d_{p, q} = \sum_{i = 1}^{N} | p_{i} - q_{i} |

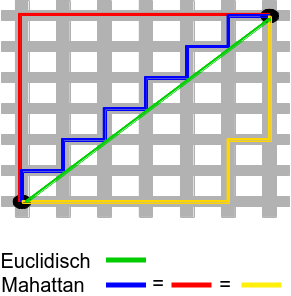
De Manhattan afstand tussen de twee zwarte punten p(0,0) en q(6,6) in Figuur hierboven, bedraagt dus: $d_{p, q} = | p_{1} - q_{1} | + | p_{2} - q_{2} | = 6 + 6 = 12$ in de vakjes 1 groot zijn.

Gestandardiseerde Euclidische afstand: Wanneer je rekening wilt houden met het feit dat de verschillende kolommen (dimensies) van je dataset mogelijk verschillende verdelingen hebben, zoals een kolom met gewichten van muizen en eentje met gewichten van olifanten, dan kan je beter eerst al je kolommen standarizeren naar Z-scores (zie hoofdstuk Spreidingsmaten).
Cosinusgelijkheid: Zoals reeds vermeld kunnen we de afstand meten tussen de uiteinden van alle vectoren m.b.v. de Euclidische afstandsformule. Met andere formules (die we hier niet behandelen) kunnen we ook de hoeken berekenen tussen de verschillende vectoren. Deze hoeken kunnen eveneens gebruikt worden als vergelijkingscriterium: hoe kleiner de hoek des te dichterbij elkaar de instanties liggen en des te meer we ervan uitgaan dat ze op elkaar lijken.
Dynamic Time Warping (DTW): is geen echt afstandcriterium in de strikte wiskundige zin van het woord, maar eerder een algoritme waarmee de gelijkheid tussen twee tijdreeksen kan bepaald worden. Dit kan kan handig zijn om bijvoorbeeld beurskoersen met elkaar te vergelijken.

Data Science 1

Afstanden meten

Contents