Forecasting#

De dataset#

Om de technieken duidelijk te maken, zullen we werken met de volgende dataset:

20, 100, 175, 13, 37, 136, 245, 26, 75, 155, 326, 48, 92, 202, 384, 82, 176, 282, 445, 181

Dit zijn de opbrengsten van een firma voor ieder kwartaal, gedurende de laatste 5 jaar. We kunnen deze data in Python inlezen met:

opbrengsten = np.array([20,100,175,13,37,
                        136,245,26,75,155,
                        326,48,92, 202,384,
                        82,176,282,445,181], dtype=float)

pd.DataFrame(opbrengsten.reshape(-1, 4),
             columns=['Q{}'.format(i) for i in range(1, 5)],
             index=['Jaar {}'.format(i) for i in range(1, 6)])
Q1 Q2 Q3 Q4
Jaar 1 20 100 175 13
Jaar 2 37 136 245 26
Jaar 3 75 155 326 48
Jaar 4 92 202 384 82
Jaar 5 176 282 445 181

Note

Voor wie geïnteresseerd is, kunnen we deze gegevens ook m.b.v. volgende code in een grafiek zetten:

import matplotlib.pyplot as plt

n = opbrengsten.size

fig, ax = plt.subplots(figsize=(10, 5))
ax.set_title('Opbrengsten voorbije 5 jaar')
ax.set_xlabel('kwartaal')
ax.set_ylabel('opbrengst (€)')
ax2 = ax.secondary_xaxis('top')
ax2.set_xticks(range(n))
ax2.set_xticklabels(['Q{}'.format(j % 4 + 1) for j in range(n)])

ax.set_xticks(range(n))
ax.plot(opbrengsten, label='gegeven', color='C0', marker='o')
for i in range(0, n, 4):
    ax.axvline(i, color='gray', linewidth=0.5)

ax.legend()
plt.show()

Dit resulteert in het volgende:
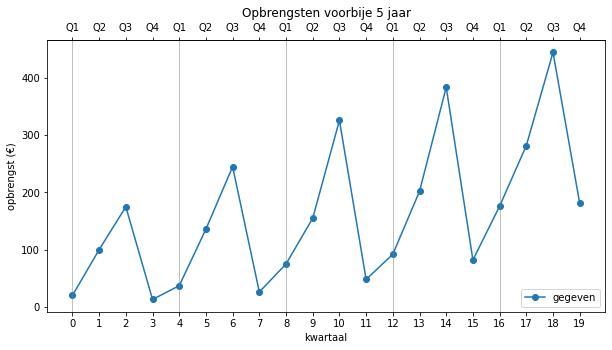
../_images/Forecasting_4_0.png

Hier zit duidelijk een regelmaat in. De opbrengsten tonen ieder jaar hetzelfde patroon en de opbrengsten stijgen ook met de tijd. In de volgende tekst gaan we een aantal modellen opstellen die proberen om een voorspelling te maken voor de volgende kwartalen. Aangezien sommige modellen beter kunnen voorspellen dan andere, hebben we ook een maat nodig om dat te bepalen. Dit wordt allemaal uitvoerig besproken.

Forecasting op basis van het verleden#

In dit deel bespreken we een paar heel eenvoudige technieken om waarden te voorspellen. Ze geven inzicht in de eigenschappen en problematiek van forecasting. Met deze modellen kan je ook tonen hoe je kan inschatten of een model goed of minder goed is (de betrouwbaarheid van de voorspelling). We bespreken volgende voorspellingstechnieken:

  • Naïeve forecasting (Naive)

  • Gemiddelde van alle vorige waarden (Average)

  • Voortschrijdend gemiddelde (Moving Average)

  • Lineaire combinatie (Linear Combination)

We zullen al deze voorspellingstechnieken onderbrengen in één Pythonscript (forecast.py) te samen met enkele functies om hun kwaliteit te beoordelen.

Naïeve forecasting#

De eerste vorm van forecasting is heel eenvoudig: we gaan ervan uit dat de laatst gemeten waarde zal blijven. In ons voorbeeld zullen we de grafiek dus aanvullen met de waarde 181 voor de volgende kwartalen. Deze voorspellingsmethode is in de praktijk niet echt zinvol, maar het is wel interessant om een aantal begrippen te tonen. We kunnen deze manier van voorspellen ook iets wiskundiger noteren. Als er n waarden zijn en als we de gegeven waarden xi noemen (waarbij i gaat van 0 tot n−1), dan is de voorspelde waarde fn gelijk aan:

fn=xn−1

In Python kunnen we deze voorspeller definiëren aan de hand van een functie. De input van deze functie is een vector met alle gegevens van het verleden en de output is de eerstvolgende voorspelde waarde (in dit geval de laatste waarde):

import numpy as np

# voorspelling is vorige waarde
def naive(y: np.array):
    if y.size > 0:
        return y[-1]
    return np.NaN

Je kan deze voorspellerfunctie dan toepassen op de gegevens:

naive(opbrengsten)

met als resultaat:

181.0

Meerdere voorspellingen maken#

Om de voorspelling verder te laten werken, kan je de voorspelde waarde iedere keer toe en gebruik je de functie weer (we voorspellen hier 4 waarden):

from scripts.forecast import naive

verleden = opbrengsten
voorspeld = np.empty()

for i in range(4):
    volgende = naive(verleden)
    voorspeld = np.append(voorspeld, volgende)
    verleden = np.append(verleden, volgende)

array([ 20., 100., 175.,  13.,  37., 136., 245.,  26.,  75., 155., 326.,
        48.,  92., 202., 384.,  82., 176., 282., 445., 181., 181., 181.,
       181., 181.])

Zoals verwacht geeft dit iedere keer weer 181 als resultaat. Bovenstaande code werkt dus, maar deze werkwijze is weinig flexibel: we moeten telkens apart opgeven welke voorspellerfunctie we willen gebruiken, en het aantal dagen dat we vooruit willen voorspellen. We schrijven daarom eerst een functie predictor die een voorspellingen kan maken met eender welke andere voorspellersfunctie (momenteel hebben we alleen nog maar naive geschreven).

Deze nieuwe functie werkt als een Python generator. Een generator kan je een beetje vergelijken met de Java Iterator-interface waarmee je over een collectie van gegevens kunt itereren.

Hieronder zie je een eenvoudige generator die positieve getallen kan genereren.

# een voorbeeld van een generator
def generator():
    i = 0
    while True:
        # yield is de output van één aanroep van de generator
        yield i*i
        i += 1

gen = generator()   # generator aanmaken

next(gen)           # waarden genereren
next(gen)
next(gen)

0

1

4

Je kan de generator ook gebruiken in een for-loop of list comprehension zoals je hieronder ziet:

gen = generator()
[next(gen) for _ in range(10)]

met als resultaat:

[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]

Een generator produceert telkens een nieuwe waarde dankzij het yield statement.

We gebruiken deze techniek nu om onze predict-generator te schrijven.

import numpy as np
# generator functie, y zijn de opbrengsten, forecast de functie
def predictor(y: np.array, f, *argv):
    i = 0
    while True:
        if i <= y.size:                     # verleden voorspellen
            yield f(y[:i], *argv)           # geef voorspelde waarde terug
        else:                               # toekomst voorspellen
            y = np.append(y, f(y, *argv))   # plak voorspelling achteraan
            yield f(y, *argv)               # geef voorspelde waarde terug
        i += 1

Onze predict-generatorfunctie heeft drie argumenten:

  1. y, een Numpy array waarvoor we voorspellingen willen doen,

  2. f de voorspellersfunctie die we willen gebruiken,

  3. optionele argumenten voor f die hier doorgegeven worden als *argv.

Zolang index i kleiner is dan lengte van y, gebruiken we onze functie f om een voorspelling te doen op alle elementen van y die voor het element met index i liggen (y[:i]). Van zodra de index groter wordt en voorbij het einde van onze voorbeeldgegevens gaat, plakken we telkens onze vorige voorspelling achteraan bij onze gegevens, waarop we dan een nieuwe voorspelling doen.

We kunnen hem als volgt gebruiken om voorspellingen te maken voor alle waarden van opbrengsten:

gen = predictor(opbrengsten, naive)
predictions = np.array([next(gen) for _ in range(20)])
predictions
Q1 Q2 Q3 Q4
Jaar 1 NaN 20.0 100.0 175.0
Jaar 2 13.0 37.0 136.0 245.0
Jaar 3 26.0 75.0 155.0 326.0
Jaar 4 48.0 92.0 202.0 384.0
Jaar 5 82.0 176.0 282.0 445.0

Omdat het niet handig is om steeds te werken met een list comprehension schrijven we nog een extra functie die de code hierboven uitvoert. We noemen deze functie predict.

import numpy as np

def predict(y: np.array, start, end, f, *argv):
    # generator aanmaken
    generator = predictor(y, f, *argv)
    # voorspellingen doen
    predictions = np.array([next(generator) for _ in range(end)])
    # opkuisen
    predictions[:start] = np.nan
    return predictions

Deze functie maakt een generator aan op basis van de gegevens y en de voorspellersfunctie f. Dan worden er voorspellingen gemaakt waarbij de enkel de delen tussen start en einde behouden blijven. De rest wordt op een NA-waarde gezet, zodat deze niet geplot zullen worden.

Het is handiger om de voorspellingen te vergelijken met de originele waarden. Dit kunnen we door ze te samen te bekijken in een DataFrame.

import pandas as pd

df = pd.concat([
    pd.Series(opbrengsten, name='opbrengsten'),
    pd.Series(predictions, name='naive')], axis=1)
df.index=range(1,21)
df.transpose()
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
opbrengsten 20.0 100.0 175.0 13.0 37.0 136.0 245.0 26.0 75.0 155.0 326.0 48.0 92.0 202.0 384.0 82.0 176.0 282.0 445.0 181.0
naive NaN 20.0 100.0 175.0 13.0 37.0 136.0 245.0 26.0 75.0 155.0 326.0 48.0 92.0 202.0 384.0 82.0 176.0 282.0 445.0

Naive forecasting kan uiteraard geen voorspelling doen voor het allereerste kwartaal, maar vanaf het tweede kwartaal zie je duidelijk dat de voorspelling gelijk is aan de vorige waarden.

Nog beter is om deze voorspellingen tonen in een grafiek (één beeld zegt meer dan blabla):

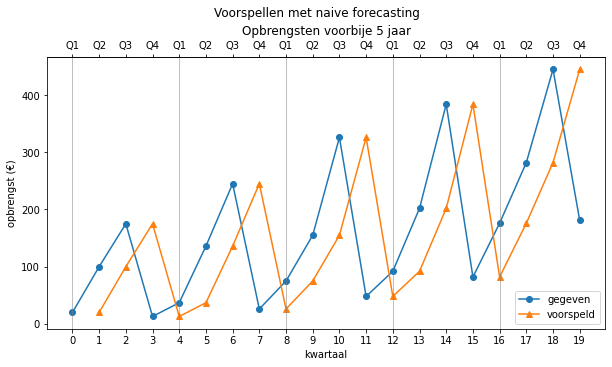
../_images/Forecasting_20_0.png

Dankzij onze predict functie kunnen we ook heel eenvoudig in de toekomst voorspellen foor de range te vergroten naar bv. 24.

predictions = predict(opbrengsten, 0, 24, naive)
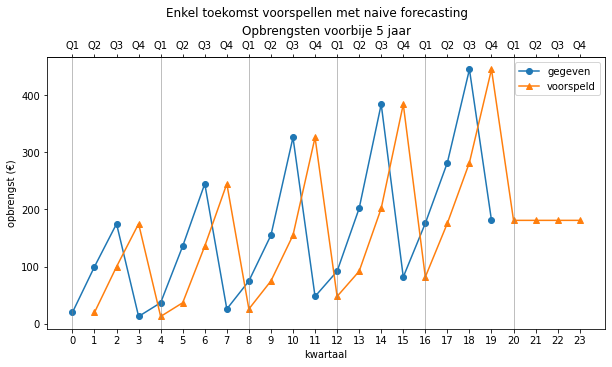
../_images/Forecasting_22_0.png

Wil je enkel de voorspellingen voor het volgende jaar (4 kwartalen) dan kan dat met deze code:

predictions = predict(opbrengsten, 20, 24, naive)

Die je ook grafisch kan voorstellen natuurlijk

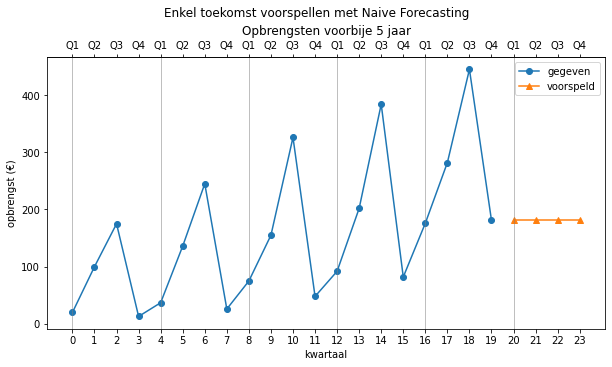
../_images/Forecasting_24_0.png

Dit model is op korte termijn misschien wel een redelijke voorspeller, maar op lange termijn zal het alleen maar erger worden, want de waarde blijft constant. Dit is een eigenschap voor alle voorspellingsmethodes: hoe verder je in de toekomst voorspelt, hoe groter de verwachte fout. Je zou dus een soort betrouwbaarheidsinterval kunnen opstellen dat steeds groter wordt, naarmate de tijd vordert. In dit document zullen we daar echter niet verder op in gaan.

Gemiddelde van alle vorige waarden#

De vorige voorspellingsmethode werkt niet goed omdat er niet echt diep in het verleden wordt gekeken. Dit kunnen we oplossen door het gemiddelde te nemen van alle voorgaande metingen en dat als voorspelling te gebruiken. Zo is de voorspelling gebaseerd op het volledige verleden.

Dit wil dus zeggen dat:

fn=1n∑i=0n−1xi

In Python kan je weer een functie maken:

# voorspelling is gemiddelde van alle vorige waarden
import numpy as np
def average(y: np.array):
    if y.size < 1:
        return np.NaN
    return y.mean()

Als we deze functie gebruiken om opeenvolgende voorspellingen te bekomen, krijgen we steeds de waarde 160 terug.

predictions = predict(opbrengsten, 20, 24, average)

array([         nan,  20.        ,  60.        ,  98.33333333,
        77.        ,  69.        ,  80.16666667, 103.71428571,
        94.        ,  91.88888889,  98.2       , 118.90909091,
       113.        , 111.38461538, 117.85714286, 135.6       ,
       132.25      , 134.82352941, 143.        , 158.89473684,
       160.        , 160.        , 160.        , 160.        ])

Grafisch levert dit:

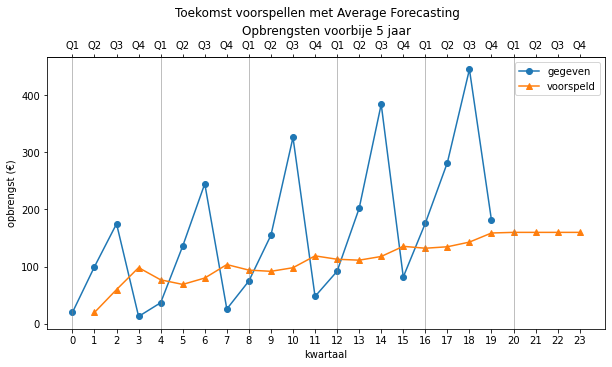
../_images/Forecasting_28_0.png

Voortschrijdend gemiddelde#

Het nadeel van de vorige methode is dat deze steeds de gehele geschiedenis meeneemt in de voorspelling. Als er recent grote wijzigingen zijn gebeurd, dan zal de voorspelling minder goed zijn. We kunnen dit veranderen door steeds het gemiddelde te nemen van de laatste m metingen. Men noemt dit het voortschrijdend gemiddelde. Er geldt dus:

fn=1m∑i=n−mn−1xi

In Python kan je dit implementeren met een functie die een extra parameter m krijgt. We kunnen ook pas een voorspelling doen als er minstens m waarden zijn.

# voorspelling is voortschrijdend gemiddelde van m vorige waarden
import numpy as np

def moving_average(y: np.array, m=4):
    if y.size < m:
        return np.NaN

    return np.mean(y[-m:])

Merk op dat deze voorspellende functie een extra parameter m heeft die standaard steeds op 4 staat. Als je hem dus vergeet mee te geven is m=4. Herinner je het *argv argument van onze generator? Die *argv is een ‘verzamelbak’ voor al extra argumenten die je aan een functie meegeeft. Voor bovenstaande functie zou hij dus de m bevatten.

Als we nu de komende 4 kwartalen willen voorspellen met onze predict functie

predict(opbrengsten, 0, 24, moving_average)

krijgen we (met m=4) de volgende waarden:

array([       nan,        nan,        nan,        nan,  77.      ,
        81.25    ,  90.25    , 107.75    , 111.      , 120.5     ,
       125.25    , 145.5     , 151.      , 155.25    , 167.      ,
       181.5     , 190.      , 211.      , 231.      , 246.25    ,
       271.      , 294.75    , 297.9375  , 261.171875])

Grafisch ziet dit er als volgt uit:

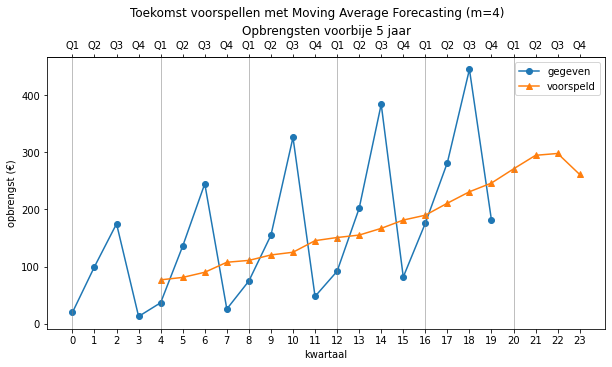
../_images/Forecasting_32_0.png

Merk op dat we ook andere waarden voor m kunnen nemen. Hieronder zie je enkele voorbeelden. Wat is de invloed van de m?

predict(opbrengsten, 0, 24, moving_average, 3)  # m = 3
predict(opbrengsten, 0, 24, moving_average, 6)  # m = 6
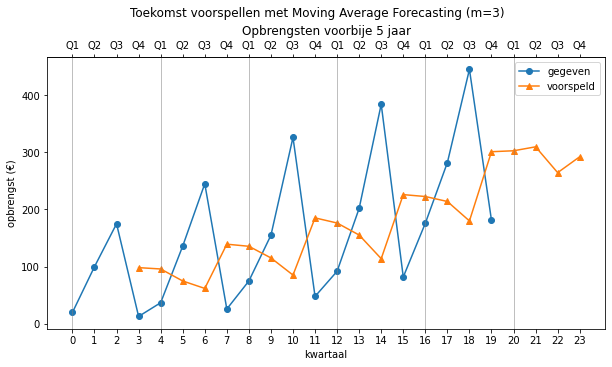
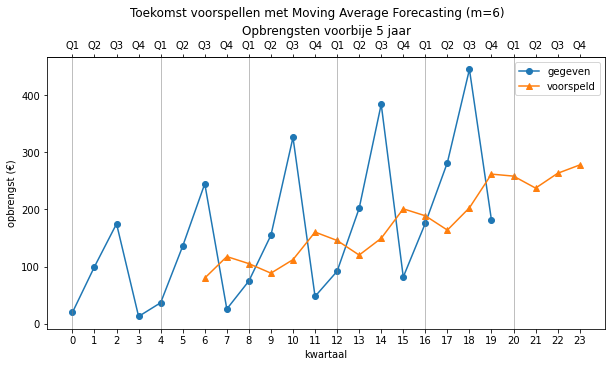
../_images/Forecasting_34_0.png ../_images/Forecasting_34_1.png

Lineaire combinatie#

We kunnen de vorige techniek nog verbeteren door een gewogen gemiddelde te berekenen in plaats van een rekenkundig gemiddelde. We gaan de volgende waarde dus voorspellen door gewichten te geven aan de vorige waarden. Deze gewichten schatten we aan de hand van het verleden. Om een voorspelling te maken, moeten we de gewichten vermenigvuldigen met de laatste m waarden en dan alles optellen. Men noemt dit een lineaire combinatie van de laatste m waarden. Lineaire combinaties worden heel veel gebruikt in machine learning technieken en zullen dus regelmatig terugkomen in deze cursus.

Er geldt nu:

fn=∑i=n−mn−1ai−n+m⋅xi

Als m=4, dan kunnen we dit ook schrijven als:

fn=a0⋅xn−4+a1⋅xn−3+a2⋅xn−2+a3⋅xn−1

We kunnen de ai (de gewichten) berekenen uit het verleden. Dat kan op verschillende manieren. De meest eenvoudige manier leert de gewichten uit de 2⋅m gegevens die voorafgaan aan degene die men wil gebruiken. Als je voor die gegevens de bovenstaande formule uitschrijft, krijg je een stelsel van m vergelijkingen met m onbekenden en dat kan je oplossen.

We gaan niet te diep in op de wiskunde van deze techniek, maar geven hier de code in Python om de gewichten te berekenen:

# voorspelling is een lineaire combinatie
import numpy as np

def bereken_gewichten(y: np.array, m: int):
    # n is aantal elementen
    n = y.size
    # we hebben > 2 * m elementen nodig
    if n < 2 * m:
        return np.NaN
    # selecteer de laatste elementen
    M = y[-(m + 1):-1]
    # maak een matrix M van coëfficiënten
    for i in range(1, m):
        M = np.vstack([M, y[-(m + i + 1):-(i + 1)]])

    # selecteer de bekenden
    v = np.flip(y[-m:])
    # los het stelsel van m vergelijkingen op
    return np.linalg.solve(M, v)

Wanneer we deze functie gebruiken, vinden we in ons geval volgende gewichten:

a = bereken_gewichten(y=opbrengsten, m=4)

array([1.0080186 , 0.13742887, 0.12600184, 0.08679208])

En deze kunnen we nu gebruiken om handmatig een voorspelling te maken volgens bovenstaande formule.

m = 4
n = opbrengsten.size
prediction = (opbrengsten[n-m:n] * a).sum()
prediction

287.94640003946205

In plaats van dit steeds handmatig te moeten doen, kunnen we dit nu weer samenvatten in een nieuwe voorspellerfunctie:

import numpy as np

def linear_combination(y: np.array, m=4):
    n = y.size
    # check op minstens 2*m gegevens
    if n < 2 * m:
        return np.NaN
    # bereken de gewichten
    a = bereken_gewichten(y, m)
    # bereken de voorspelde waarde en geef de voorspelde waarde terug
    return np.sum(y[-m:] * a)

Je kan deze functie als volgt gebruiken om waarden te voorspellen:

prediction = linear_combination(opbrengsten)
prediction

met hetzelfde resultaat als tevoren natuurlijk:

287.94640003946205

Als je 4 opeenvolgende waarden voorspelt door gebruik te maken van de generator

predict(opbrengsten, 0, 24, linear_combination)  # m = 3

dan vind je deze waarden:

array([         nan,          nan,          nan,          nan,
                nan,          nan,          nan,          nan,
        64.37375462, 185.06661482, 347.74993101,  39.00416917,
       135.71642907, 172.45094295, 433.52852524,  76.26132534,
       115.46692155, 262.29756407, 462.91536762, 139.89145584,
       287.94640004, 393.214892  , 543.85261675, 318.7714138 ])

Merk op dat we 8 waarden moeten wachten alvorens we een eerste voorspelling kunnen doen. Waarom 8?

Grafisch ziet dit er als volgt uit:

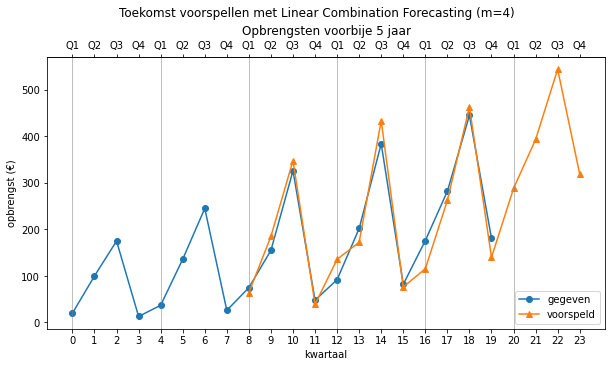
../_images/Forecasting_46_0.png

Dit lijkt een hele goede voorspeller, maar hebben we een tikkeltje vals gespeeld door m=4. Vier is namelijk duidelijk de periode waarin de herhaling zich voordoet. Wat gebeurt als we een andere waarde kiezen (m=5)?

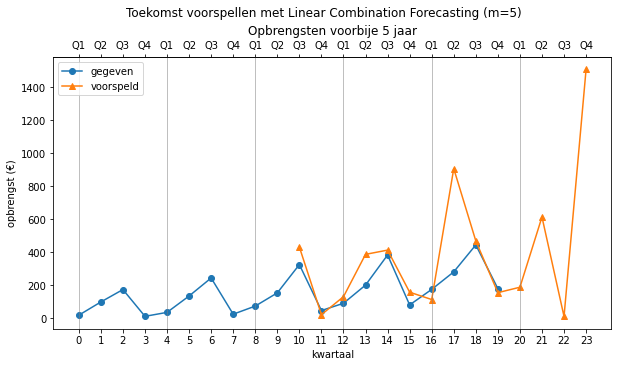
../_images/Forecasting_48_0.png

Dat ziet er al minder fraai uit. Voor waarden lager dan 4 is de situatie nog slechter. Voor 8 valt het dan weer beter mee…

Een algemeen probleem is dat we momenteel nog niet weten hoe goed elke voorspeller is. We kunnen er geen waarde op plakken. Vandaar dat we dat probleem nu eerst gaan aanpakken in de volgende paragraaf.

Betrouwbaarheid van een model#

Alvorens verder te gaan met andere voorspellingsmethoden, willen we eerst kunnen meten hoe goed een model kan voorspellen. Maar dan hebben we data uit de toekomst nodig en die hebben we niet. Een oplossing bestaat erin om het model toe te passen op eerdere gegevens en kijken hoe goed het de vorige gegevens had kunnen voorspellen. Zo kunnen we de betrouwbaarheid van het model inschatten.

Dat is exact wat we gaan doen. We nemen opeenvolgende kwartalen en laten dit model steeds de toekomst voorspellen. We kijken naar het verschil tussen de voorspelde waarde en de echte waarde. De originele waarden duiden we weer aan met xi.

De voorspelde waarden noemen we, naar analogie met voorgaande, fi.

Voor naïeve forecasting krijgen we dus: fi=xi−1, maar f0 bestaat niet omdat er geen x−1 is. Vanaf f1 kunnen we de waarden uitrekenen.

In Python kunnen we deze waarden ook uitrekenen met onze eerder geschreven generator. Met de generator functie kunnen we nu dus alle voorspellingsfuncties los laten op het verleden met volgende code. We verzamelen ook alles in één dataframe.

opbrengsten naive average moving_average linear_combination
f0 20.0 NaN NaN NaN NaN
f1 100.0 20.0 20.000000 NaN NaN
f2 175.0 100.0 60.000000 NaN NaN
f3 13.0 175.0 98.333333 NaN NaN
f4 37.0 13.0 77.000000 77.00 NaN
f5 136.0 37.0 69.000000 81.25 NaN
f6 245.0 136.0 80.166667 90.25 NaN
f7 26.0 245.0 103.714286 107.75 NaN
f8 75.0 26.0 94.000000 111.00 64.373755
f9 155.0 75.0 91.888889 120.50 185.066615
f10 326.0 155.0 98.200000 125.25 347.749931
f11 48.0 326.0 118.909091 145.50 39.004169
f12 92.0 48.0 113.000000 151.00 135.716429
f13 202.0 92.0 111.384615 155.25 172.450943
f14 384.0 202.0 117.857143 167.00 433.528525
f15 82.0 384.0 135.600000 181.50 76.261325
f16 176.0 82.0 132.250000 190.00 115.466922
f17 282.0 176.0 134.823529 211.00 262.297564
f18 445.0 282.0 143.000000 231.00 462.915368
f19 181.0 445.0 158.894737 246.25 139.891456
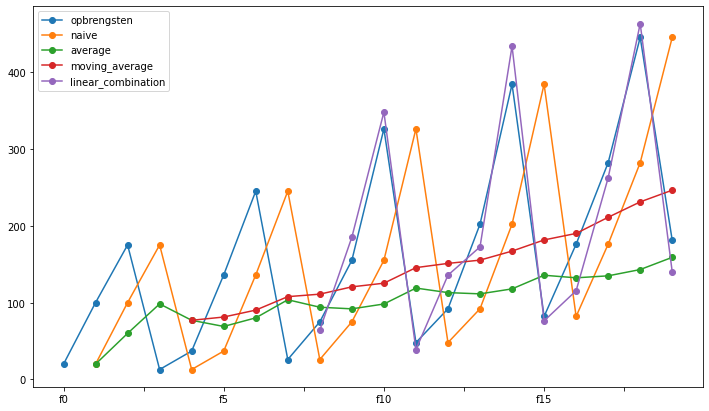
../_images/Forecasting_50_1.png

De blauwe lijn zijn de originele waarden, en voor naïve forecasting (oranje) is die het origineel maar 1 plaats opgeschoven (de eerste voorspelling bestaat niet omdat er nog geen verleden was). De andere voorspellingsfuncties zijn ook afgebeeld. De lineaire combinatie is zelfs zo goed dat ze op het einde overlapt met de originele opbrengsten.

Als we voor elke voorspellingsfunctie de voorspelde waarde aftrekken van de echte waarde, krijgen we de fout. Deze noteren we met ei.

Er geldt dus dat fout voor de i-de voorspelling van een voorspellingsfunctie gelijk is aan:

ei=xi−fi

De fouten voor alle voorspellingsfuncties en voor alle tijdstippen is dus gelijk aan volgende tabel:

naive average moving_average linear_combination
f0 NaN NaN NaN NaN
f1 -80.0 -80.000000 NaN NaN
f2 -75.0 -115.000000 NaN NaN
f3 162.0 85.333333 NaN NaN
f4 -24.0 40.000000 40.00 NaN
f5 -99.0 -67.000000 -54.75 NaN
f6 -109.0 -164.833333 -154.75 NaN
f7 219.0 77.714286 81.75 NaN
f8 -49.0 19.000000 36.00 -10.626245
f9 -80.0 -63.111111 -34.50 30.066615
f10 -171.0 -227.800000 -200.75 21.749931
f11 278.0 70.909091 97.50 -8.995831
f12 -44.0 21.000000 59.00 43.716429
f13 -110.0 -90.615385 -46.75 -29.549057
f14 -182.0 -266.142857 -217.00 49.528525
f15 302.0 53.600000 99.50 -5.738675
f16 -94.0 -43.750000 14.00 -60.533078
f17 -106.0 -147.176471 -71.00 -19.702436
f18 -163.0 -302.000000 -214.00 17.915368
f19 264.0 -22.105263 65.25 -41.108544

Als ons model de toekomst perfect voorspelt, dan zijn alle ei=0. Als het model minder goed is, dan worden de waarden van ei groter (of kleiner als ze negatief zijn). Je kan uit bovenstaande tabel dus al meteen een intuïtief idee krijgen van welke model het beste zal zijn door de te kijken naar de grootte van de fouten.

We kunnen nu de gemiddelde fout proberen te berekenen. Dat is dan een maat voor de betrouwbaarheid van onze voorspeller, maar we kunnen dit niet doen door zomaar een gewoon gemiddelde te nemen, want de sommige ei zijn negatief. Dit gemiddelde kan je op verschillende andere manieren berekenen waarbij de ei telkens positief gemaakt worden:

  • de MAE (Mean Absolute Error) = 1n∑i=0n−1|ei|

  • de RMSE (Root Mean Squared Error) = 1n∑i=0n−1ei2

  • de MAPE (Mean Absolute Percentage Error) = 1n∑i=0n−1|eixi|

Bemerk dat de formule voor RMSE enorm lijkt op de formule voor standaardafwijking en ook op de formule voor standaardschattingsfout (zie regressie). Het is een veelgebruikte formule om een gemiddelde fout te berekenen. De waarden van MAE en RMSE zijn echter moeilijk te interpreteren. Dat komt omdat de fout bij heel grote waarden ook heel groot kan worden. We zijn dus meer geïnteresseerd in de fout ten opzichte van de oorspronkelijke data. Vandaar dat de MAPE dikwijls gebruikt wordt, maar het nadeel van deze maat is dat de waarden xi niet 0 mogen worden. Als dit het geval is, kan je dus toch enkel maar de MAE en RMSE berekenen.

In Python kunnen we deze fouten als volgt berekenen op basis van de originele waarde x en de voorspellingen f.

import numpy as np

# x en f zijn Numpy arrays
# x is origineel, f is voorspelling
e = x - f

# nanmean is gemiddelde zonder NA-waarde
mae = np.nanmean(np.abs(e))
# ** 2 is tweede macht
rmse = np.sqrt(np.nanmean(e ** 2))

mape = np.nanmean(np.abs(e / x))

Enkele voorbeelden

x = opbrengsten
f = predict(opbrengsten, 0, 20, naive)

e = x -f
mae = np.nanmean(np.abs(e))
rmse = np.sqrt(np.nanmean(e ** 2))
mape = np.nanmean(np.abs(e / x))

Dit geeft de volgende resultaten voor Naïeve Forecasting:

MAE = 137.42105263157896 
RMSE = 158.6978260720669 
MAPE = 2.0702566894377608

Als je naar de MAPE kijkt, zie je dat de voorspelling gemiddeld dus 207% afwijkt van de echte waarde. Dit is dus niet zo’n goede voorspeller … (maar dat wisten we intuïtief al).

We maken een functie die al deze grootheden kan berekenen. Dat zou er als volgt uit kunnen zien:

import numpy as np

def forecast_errors(x: np.array, f: np.array, method: str):
    e = x - f
    mae = np.nanmean(np.abs(e))
    rmse = np.sqrt(np.nanmean(e ** 2))
    mape = np.nanmean(np.abs(e / x))
    return pd.DataFrame({'MAE': [mae], 'RMSE': [rmse], 'MAPE': [mape]}, index=[method])

Je gebruikt deze functie als volgt (bijvoorbeeld voor het voortschrijdend gemiddelde):

x = opbrengsten
f = predict(opbrengsten, 0, 20, moving_average)

forecast_errors(x, f, 'moving average')

met als resultaat:

MAE RMSE MAPE
moving average 92.90625 113.321342 0.77707

Als je alles goed hebt geïmplementeerd, zou je volgende waarden moeten vinden:

MAE RMSE MAPE
naive 137.421053 158.697826 2.070257
average 103.004796 130.806207 1.036220
moving average 92.906250 113.321342 0.777070
linear combination 28.269228 32.792905 0.174283

De lineaire combinatie geeft dus in dit geval het beste resultaat (zoals we grafisch al konden zien). De voorspelde waarde wijkt gemiddeld ongeveer 17% af van de echte waarde.

Een model maken voor de data#

Bij de vorige voorspellingsmethodes, probeerden we de volgende waarde te voorspellen aan de hand van het verleden. Maar dat kan ook anders. Je kan ook een model opstellen dat de wetmatigheden in de data beschrijft. Je kan dit model dan gebruiken om voorspellingen te doen, maar ook om het verleden te modelleren. Je zoekt dus een formule of functievoorschrift die het gedrag van de data weergeeft. Het voordeel van een model is dat het ook kan uitleggen waarom de data zich op een bepaalde manier gedraagt. We zien hier 3 technieken:

  • trend forecasting,

  • seasonal forecasting en

  • seasonal trend forecasting.

Trend forecasting#

De eenvoudigste manier om een model op te stellen, is door een lijn te zoeken die door de data gaat. Dit kunnen we doen met regressie. Dit kan lineaire regressie zijn, maar natuurlijk ook niet-lineaire regressie. Het model dat uit de regressie komt, is eigenlijk ook een voorspeller. We gaan ervan uit dat onze data een functie is van de tijd en daarom zetten we de nummers 0…(n−1) in de X-as. Die symboliseren het tijdstip.

In Python gaan we dus geen functie meer maken die de “volgende waarde” berekent. In plaats daarvan maken we een functie die een functie als return-value geeft (het model). Die laatste functie kan je gebruiken om te voorspellen. Voor lineaire regressie kunnen we bijvoorbeeld volgende functie maken (we maken gebruik van de functie general_regression() uit het deel over regressie):

# trend model
import numpy as np
from scripts.forecast import GeneralRegression

def create_trend_model(y):
    # we bouwen een lineaire regressie model
    X = np.arange(0, y.size)
    model = GeneralRegression()
    model.fit(X, y)

    # we geven een voorspellersfunctie terug
    return lambda x: model.predict([[x]])

Je kan deze functie als volgt gebruiken:

predict_trend = create_trend_model(opbrengsten)
predict_trend(20)

met als resultaat

array([282.32105263])

We kunnen dit ook handmatig doen (zie leerstof Samenhang). In ons voorbeeld vinden dan we volgende formule voor de regressielijn:

fi=49.3286+11.6496⋅i

Als we dus een voorspelling willen doen voor het eerstvolgende kwartaal (i=20), dan vinden we:

49.3286+11.6496⋅20=282.3206

Wanneer we dit model zowel in het verleden als de toekomst gebruiken, krijgen we grafisch dit:

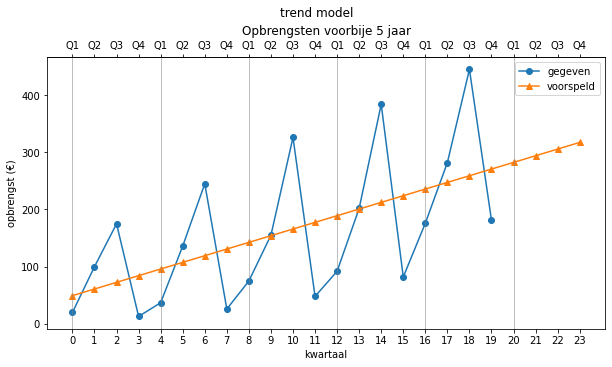
../_images/Forecasting_62_0.png

Als we nu de betrouwbaarheid van dit model willen bepalen, passen we de functie toe op het verleden en vergelijken de gevonden waarden met de echte waarden:

forecast_errors(opbrengsten, predict_trend(range(20)), 'trend model')
MAE RMSE MAPE
trend model 85.0 100.616689 1.149211

Merk op dat de RMSE exact gelijk is aan de standaardschattingsfout (se) van de regressie (kijk zelf maar na). De berekening is namelijk dezelfde.

Bemerk dat je de MAE, RMSE en MAPE ook zou kunnen berekenen door het model steeds opnieuw op te stellen voor opeenvolgende waarden (zoals hierboven werd gedaan). We kiezen in dit document echter om het berekende model te gebruiken in het verleden omdat we niet verwachten dat dit model veel zal veranderen naarmate er meer data beschikbaar komt. Als dit toch het geval is, moet je dus steeds een nieuw model opstellen, naarmate er meer data beschikbaar is.

Dit model is niet zo heel goed. De voorspelde waarden volgen een rechte lijn, terwijl de echte waarden steeds meer schommelen rond die lijn. Daardoor wordt de fout ook steeds groter. Dit model kan die variaties niet goed voorspellen en is enkel bruikbaar als de oorspronkelijke data gelijkmatiger verandert. Als we ook de schommelingen willen meenemen, hebben we nood aan een ander model. Dit bespreken we hieronder.

Seasonal forecasting#

Het principe#

Bij seasonal forecasting gaan we ongeveer op dezelfde manier te werk als bij regressie. We zoeken namelijk een soort formule (een model) waarmee we voorspellingen kunnen doen. We gebruiken alleen geen lijn, maar een ander model.

Tijdsgebonden data bestaat namelijk meestal uit een aantal componenten:

  • een (al dan niet lineaire) trend (stijgend of dalend)

  • een seizoensgebonden trend (een patroon dat om de zoveel metingen steeds terug komt)

  • een niet regelmatige component (we beschouwen dit als ruis die niet te voorspellen is)

We kunnen er nu vanuit gaan dat elk datapunt gelijk is aan de som van deze componenten. We krijgen dus:

data=trend+seizoen+ruis

Of meer wiskundig:

xi=T(i)+S(i)+R(i)

Dit noemt men een additief decompositiemodel.

Dikwijls worden de seizoensschommelingen groter als de waarden zelf groter worden. Je kan dit zien in het voorbeeld van de opbrengsten: als de opbrengsten groter worden, dan worden de schommelingen ook groter. In dat geval gebruik je beter het multiplicatief decompositiemodel. Dit ziet er als volgt uit:

xi=T(i)⋅S(i)⋅R(i)

We zijn het meest geïnteresseerd in de formules voor T(i) en S(i) aangezien R(i) niet te voorspellen is. We kunnen T(i) en S(i) dan gebruiken om voorspellingen te maken.

Het bepalen van de seizoensgrootte#

Om de formules voor T(i) en S(i) te vinden, moeten we weten hoe groot een seizoen is (de grootte van het wederkerend patroon). In vele gevallen is dit al bekend. In ons voorbeeld hebben we de cijfers per kwartaal genoteerd. We verwachten dus een patroon dat zich ieder jaar, en dus iedere 4 kwartalen, herhaalt. Dat is ook heel duidelijk zichtbaar in de grafiek.

Als je niet weet wat de grootte van een seizoen is, dan kan je dit soms wel vinden via “autocorrelatie”. We gaan het signaal (de gemeten data) correleren met zichzelf, maar dan verplaatst in de tijd. Als we het signaal verplaatsen over dezelfde afstand als een seizoen, dan zal de correlatie hoger zijn. We gaan als volgt te werk:

fig, ax = plt.subplots(figsize=(10, 5))
lags, acfs, _, _ = ax.acorr(opbrengsten)
ax.set_xticks(range(-10, 11))
ax.set_xlabel('offset')
ax.set_ylabel('correlatie')
ax.set_title('Auto-correlation opbrengsten')

Deze plot een grafiek met alle autocorrelatie waarden. De grafiek van de autocorrelaties ziet er in ons voorbeeld als volgt uit:

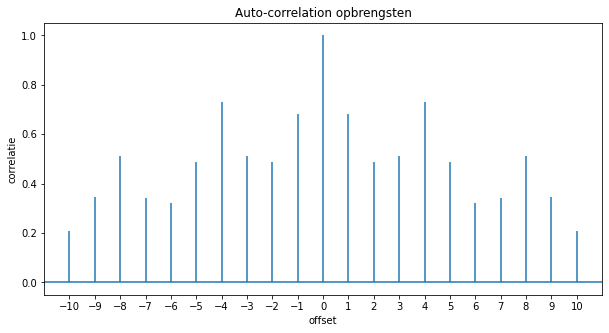
../_images/Forecasting_66_0.png

Er is een duidelijke piek bij i=0, maar dat is normaal want de waarden correleren nl. perfect met zichzelf. Er is echter ook een piek voor i=4 en i=−4. Dat wil zeggen dat het signaal, verschoven over 4 tijdseenheden naar voor of achter, sterk lijkt op het oorspronkelijke signaal. De periode van een seizoen is dus 4. Autocorrelatie werkt niet altijd even goed, dus zal je in veel gevallen handmatig moeten bepalen wat de seizoensgrootte is. Gelukkig is dit in de praktijk meestal wel eenvoudig te bepalen.

Je kan de periode dus afleiden uit de autocorrelatie grafiek, maar we kunnen hem ook vinden door alle correlaties te laten berekenen met een Numpy functie en vervolgens op zoek te gaan naar de 2e hoogste waarden (de hoogste waarde komt overeen met een verschuiving 0).

def find_period(y: np.array, maxlags=10, top_n=1) -> int:
    # autocorrelatie aan beide zijden
    acfs = np.correlate(y, y, mode='full') / np.sum(y ** 2)
    # midden bepalen
    middle = acfs.size // 2
    # omgekeerde argsort vanaf (midden + 1) tot maxlags + top selectie
    return (np.argsort(-1 * acfs[middle + 1: middle + maxlags]) + 1)[:top_n]

m = find_period(opbrengsten)
m                       # m is de periode

We vinden dus een periode van m=4.

m = [4]

Je kon dit ook vinden uit de acfs die matplotlib ax.acorr - functie teruggeeft.

Het bepalen van de trend#

Om de waarden van T(i) en S(i) te vinden, zijn er verschillende technieken.

Meestal begint men met het zoeken van T(i). Dit is de trend in de grafiek, zonder de ruis en zonder het weerkerend patroon. We kunnen deze trend gemakkelijk vinden omdat volgende eigenschappen gelden:

  • seizoenen hebben een hogere frequentie dan de trend

  • de ruis heeft een nog hogere frequentie

Als we dus de hoge frequenties wegfilteren, dan vinden we de waarden van de trend. Dit kunnen we doen door het voortschrijdend gemiddelde te nemen van steeds m getallen (waarbij m de seizoensgrootte is). Als je het gemiddelde neemt van m getallen waarbij m de grootte van een seizoen is, dan filter je alle seizoenen en de ruis weg.

In Python zullen we 2 functies maken om dit te faciliteren:

def smooth(y: np.array, m: int):
    result = np.empty(0)
    for i in range(y.size - m + 1):
        result = np.append(result, [np.mean(y[i:i + m])])

    return result

def find_trend(y: np.array, m: int):
    result = smooth(y, m)
    nan = [np.nan] * int(m / 2)
    if m % 2 == 0:
        result = smooth(result, 2)
        result = np.hstack([nan, result, nan])

    return result

De functie smooth() zal het voortschrijdend gemiddelde berekenen van een reeks getallen. Dat levert een nieuwe reeks op met n−m+1 waarden (je hebt namelijk minstens m waarden nodig om te kunnen starten).

We willen de nieuwe waarden echter terug uitlijnen met de oorspronkelijke waarden. We zoeken dus de index waarmee we ieder gemiddelde mee associeren. Als m oneven is, is dat niet zo moeilijk. Stel dat m=3, dan zal het eerst gevonden gemiddelde (het gemiddelde van waarden 0, 1 en 2) op index 1 worden geplaatst. Maar als m even is, komt dat niet uit.

Het eerst gevonden gemiddelde moet dan op index 1.5 komen (als m=4). Om dat op te lossen wordt het resultaat terug gefilterd, maar nu per 2 waarden.

Het resultaat is als volgt:

trend = find_trend(opbrengsten, 4)
trend

array([    nan,     nan,  79.125,  85.75 ,  99.   , 109.375, 115.75 ,
       122.875, 135.375, 148.25 , 153.125, 161.125, 174.25 , 185.75 ,
       200.5  , 221.   , 238.625, 258.625,     nan,     nan])
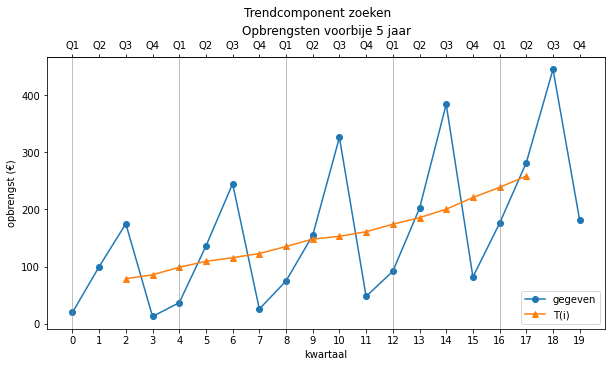
../_images/Forecasting_71_1.png

Er worden op deze manier altijd ⌊m/2⌋ nan-waarden aan beide zijden toegevoegd.

Nu we de waarden van T(i) kennen, kunnen we verder gaan met het zoeken naar S(i). Het verschil (of het quotiënt als we de multiplicatieve vorm gebruiken) tussen het gefilterde signaal en het originele signaal levert dus een signaal waar enkel nog de oscillaties van de seizoenen en de ruis in zitten. We doen dus:

  • S(i)+R(i)=xi−T(i) (additief)

  • S(i)⋅R(i)=xi/T(i) (multiplicatief)

Het bepalen van het seizoen#

Uit dit signaal (zonder de trend) willen we het patroon (het seizoen) halen dat steeds weerkeert, nl. S(i). Aangezien we de seizoensgrootte kennen, gaan we als volgt te werk: we delen het signaal op in m groepjes met punten die steeds m-stappen van elkaar liggen. Dan nemen we de gemiddelde waarde van ieder groepje. Zo vinden we m waarden die een patroon vormen dat gemiddeld voorkomt in het signaal. Dit is S(t). Je ziet dit proces hier grafisch (we nemen het gemiddelde van iedere groep):

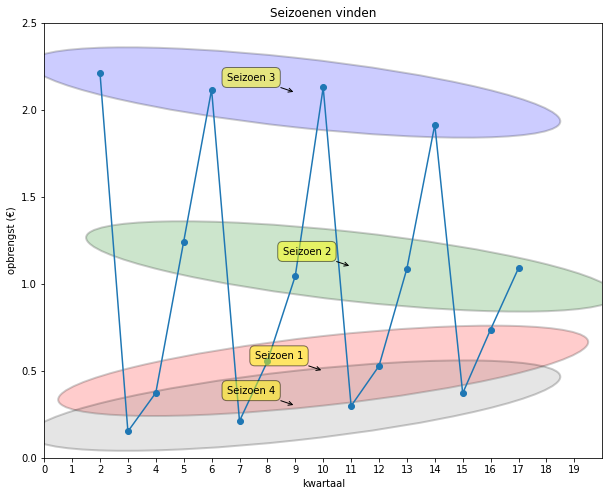
../_images/Forecasting_73_0.png

In Python kan je het seizoen met de volgende functie vinden:

import numpy as np

def find_seasons(y: np.array, m: int, method='additive'):
    if method == 'multiplicative':
        seizoen_ruis = y / find_trend(y, m)
    else:
        seizoen_ruis = y - find_trend(y, m)

    n = seizoen_ruis.size

    seizoens_patroon = np.empty(0)
    # m groepjes middellen die telkens m stappen uit elkaar liggen
    for i in range(m):
        seizoens_patroon = np.append(seizoens_patroon, np.nanmean(seizoen_ruis[np.arange(i, n, m)]))

    # patroon herhalen over volledige periode
    return np.tile(seizoens_patroon, n // m)  # n // m is het aantal seizoenen.

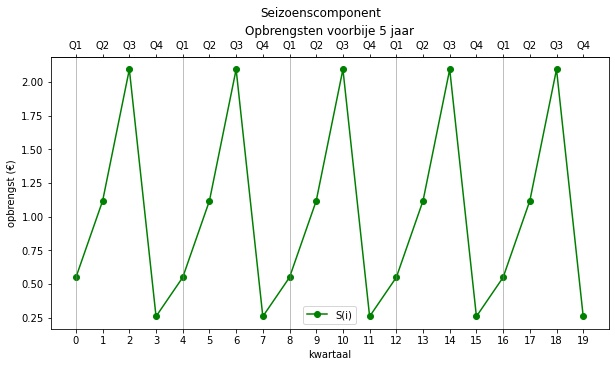
Met tile functie herhalen we het gevonden seizoenspatroon 5 maal (n // m) waardoor we het volgende resultaat krijgen.

seizoenen = find_seasons(opbrengsten, 4, method='multiplicative')
seizoenen.reshape(-1,4)

Herken je het patroon?

array([[0.54832249, 1.11670619, 2.09312815, 0.25803668],
       [0.54832249, 1.11670619, 2.09312815, 0.25803668],
       [0.54832249, 1.11670619, 2.09312815, 0.25803668],
       [0.54832249, 1.11670619, 2.09312815, 0.25803668],
       [0.54832249, 1.11670619, 2.09312815, 0.25803668]])
../_images/Forecasting_75_1.png

Het bepalen van de ruis#

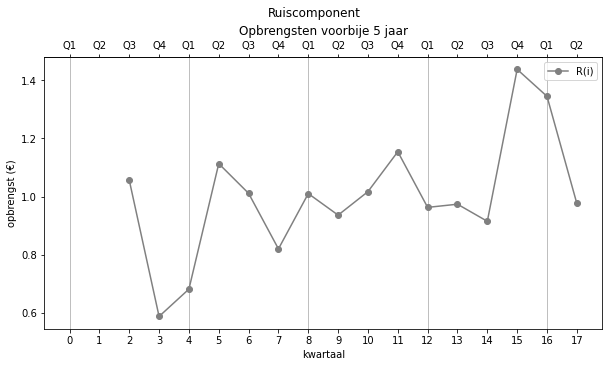
Nu we ook de waarden van het patroon hebben, kunnen we de ruis bepalen:

  • R(i)=xi−T(i)−S(i) (additief)

  • R(i)=xi/T(i)/S(i) (multiplicatief)

In ons multiplicatief voorbeeld doen we dus:

ruis = opbrengsten / trend / seizoenen
ruis

array([       nan,        nan, 1.05664355, 0.58752693, 0.68160139,
       1.11347871, 1.01122842, 0.82002741, 1.01038463, 0.93626345,
       1.01712816, 1.15450777, 0.96289511, 0.97383106, 0.91499986,
       1.4379379 , 1.34511887, 0.97642678,        nan,        nan])
../_images/Forecasting_77_1.png

We hebben nu alle componenten van het signaal ontleed en je kan nagaan of de waarden kloppen door alles weer te vermenigvuldigen (of op te tellen als je additief werkt):

trend * seizoenen * ruis # moet gelijk zijn aan opbrengsten

array([ nan,  nan, 175.,  13.,  37., 136., 245.,  26.,  75., 155., 326.,
        48.,  92., 202., 384.,  82., 176., 282.,  nan,  nan])

Dit zijn inderdaad de waarden van “opbrengsten”. Er zijn een paar waarden die we niet terug vinden omdat het voortschrijdend gemiddelde pas vanaf waarde 4 (de waarden van m) berekend kon worden.

Al deze handelingen zijn nogal veel werk. Je kan dit natuurlijk ook in een functie zetten, maar gelukkig hebben een aantal programmeurs dit al gedaan in Python. In de praktijk zullen we deze functie dus gebruiken ipv de berekeningen hierboven.

Je gaat als volgt te werk:

from statsmodels.tsa.seasonal import seasonal_decompose

sd_model = seasonal_decompose(opbrengsten, model='multiplicative', period=4)

# de verschillende componenten van het model zitten in trend, seasonal en resid
sd_model.trend
sd_model.seasonal.reshape(-1, 4)
sd_model.resid

array([    nan,     nan,  79.125,  85.75 ,  99.   , 109.375, 115.75 ,
       122.875, 135.375, 148.25 , 153.125, 161.125, 174.25 , 185.75 ,
       200.5  , 221.   , 238.625, 258.625,     nan,     nan])

array([[0.54611163, 1.11220357, 2.08468854, 0.25699626],
       [0.54611163, 1.11220357, 2.08468854, 0.25699626],
       [0.54611163, 1.11220357, 2.08468854, 0.25699626],
       [0.54611163, 1.11220357, 2.08468854, 0.25699626],
       [0.54611163, 1.11220357, 2.08468854, 0.25699626]])

array([       nan,        nan, 1.06092125, 0.58990546, 0.68436077,
       1.11798649, 1.01532226, 0.82334719, 1.01447505, 0.9400538 ,
       1.02124588, 1.15918165, 0.96679327, 0.9777735 , 0.91870413,
       1.44375922, 1.35056442, 0.98037972,        nan,        nan])

Behalve de eerste waarde van de ruiscomponenten komt alles overeen met onze eigen berekeningen.

Om het resultaat te plotten, kan je volgend commando gebruiken:

sd_model.plot()

Als je meer controle wil over de plot, kan je hem ook zelf bouwen:

def plot_seasonal_decompositon(sd_model, title: str):
    fig, axes = plt.subplots(nrows=4, ncols=1, figsize=(8, 8))

    axes[0].plot(sd_model.observed, 'o-', label='observed')
    axes[0].set_ylabel('observed')
    axes[0].set_title(title)
    axes[0].legend()

    axes[1].plot(sd_model.trend, 'o-', color='orange', label='trend')
    axes[1].set_ylabel('trend')
    axes[1].legend()

    axes[2].plot(sd_model.seasonal, 'o-', color='green', label='seasonal')
    axes[2].set_ylabel('season')
    axes[2].legend()

    axes[3].scatter(range(sd_model.nobs[0]), sd_model.resid, color='darkgrey',
                    label='noise')
    axes[3].set_ylabel('residue')
    axes[3].set_xlabel('kwartaal')
    axes[3].legend()

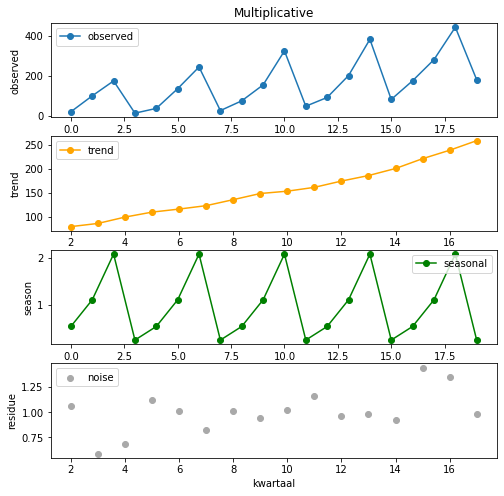
plot_seasonal_decompositon(sd_model, 'Multiplicative')

In dit geval hebben we ineens een exponentiële regressielijn door de trend berekend en geplot (meer informatie hieronder). Het resultaat is als volgt:

../_images/Forecasting_83_0.png

Voorspellingen maken met de decompositie componenten#

Als we voorspellingen willen maken, dan gaan we de grafiek van de trend verder zetten en het patroon verder herhalen. De ruis kunnen we natuurlijk niet voorspellen, dus laten we deze weg.

Om de trend verder te kunnen zetten, kunnen we een regressie uitvoeren op de trend T zodat we een formule hebben om toekomstige T(i) te kunnen berekenen. Een lineaire regressie levert bijvoorbeeld volgende formule:

T(i)=a+b⋅i

Zoals je hieronder ziet, blijkt in dit geval echter een exponentiële regressie de beste match te geven (R2 is hier gelijk aan 0.992816, wat zeer hoog is). We vinden de lijn als volgt:

X = np.arange(2, 18)                        # geen NA-waarde opnemen
y = sd_model.trend[2:18]                    # daarom van 2 tot 18

reg_model = GeneralRegression(exp=True)     # ons eigen GeneralRegression klasse
reg_model.fit(X, y)

print('R² =', reg_model.r2_score)
print('a =', reg_model.intercept_)
print('b =', reg_model.coef_)

R² = 0.9928163829760805
a = 4.276010969603498
b = [0.         0.07495604]

De gevonden functie voor T(i) is dus:

T(i)=e4,27601+0,074956⋅i

Om een voorspelling te doen, gaan we het patroon herhalen en vermenigvuldigen (omdat we multiplicatief werken) met de trend. In Python doe je dit als volgt door gebruik te maken van de predict-methode van de GeneralRegression klasse in combinatie met het seizoenspatroon van het seasonal decomposition model:

predictions = reg_model.predict(np.arange(20, 24)) * sd_model.seasonal[0:4]

Met het regressie model voorspellen we trend 4 kwartalen vooruit, en daarop superponeren we het seizoenspatroon. We kunnen ook hier weer een functie schrijven die deze voorspellingen doet o.b.v. een regressie model en een seasonal decomposition model.

# voorspellen met behulp van seasonal decomposition componenten
def seasonal_decomposition_forecast(reg_model: GeneralRegression, sd_model,
                                    start, end, method='additive', m=None):
    if not m:
        m = find_period(sd_model.observed)

    # seizoenen voldoende herhalen tot voorbij 'end'
    seasonal = np.tile(sd_model.seasonal[0:m], end // m + 1)
    if method.startswith('m'):
        return reg_model.predict(np.arange(start, end)) * seasonal[start:end]
    else:
        return reg_model.predict(np.arange(start, end)) + seasonal[start:end]


# gebruik
predictions = seasonal_decomposition_forecast(reg_model, sd_model, 20, 24, method='multiplicative')
predictions

We gebruiken de Numpy tile-functie om het seizoenspatroon voldoende malen te herhalen.

predictions = [175.94999791 386.22921653 780.2881482  103.67967675]

Ons regressiemodel, reg_model houdt automatisch rekening met het exponentieel maken van de output door de resultaten van een lineaire regressie door een exponentiële functie sturen. De voorspelde waarden volgens dit model zie je in deze grafiek:

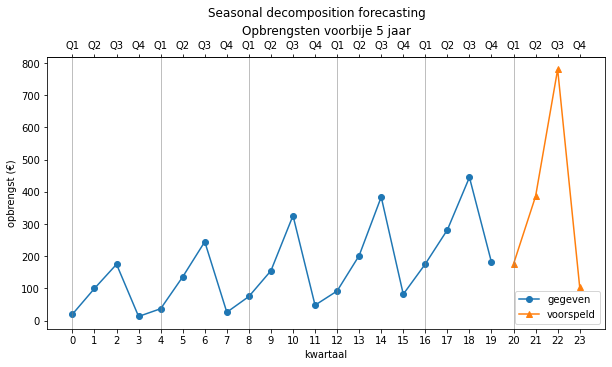
../_images/Forecasting_90_0.png

Zoals je ziet, is dit een vrij goede voorspeller. We kunnen nu ook de kwaliteit van deze voorspeller bepalen door er het verleden mee te voorspellen.

predictions = seasonal_decomposition_forecast(reg_model, sd_model,
                                              0, 20, method='multiplicative')
forecast_errors(opbrengsten, predictions, 'seasonal decomposition')

We vinden volgende waarden:

MAE RMSE MAPE
seasonal decomposition 24.29068 41.807111 0.22919
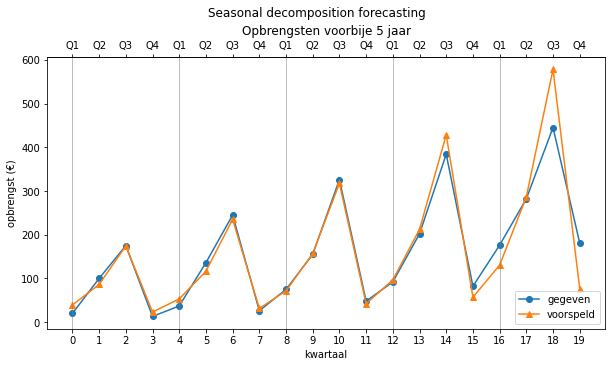
../_images/Forecasting_92_1.png

Deze voorspeller is (in dit geval) dus bijna even goed als de lineaire combinatie, maar eigenlijk is dit niet correct.

Weet je ook waarom? Denk eerst even na alvorens je verder leest.

De componenten van de seasonal decomposition (trend en seasonal) zijn gevonden o.b.v. de opbrengstgegevens zelf. Het is daarom nogal wiedes dat die goede voorspellingen produceren aangezien ze alle gegevens “op voorhand” hebben kunnen “bestuderen”. Ze konden als het ware in de toekomst kijken. Het enige wat niet het model opgenomen is, is de ruis, en daarom maakt het nog wat fouten. We moeten bovenstaande cijfers dan ook met een grove korrel zout nemen.

Seasonal trend forecasting#

Bij de vorige techniek proberen we eerst de algemene trend te bepalen en zetten daarop een patroon. Maar je kan ook direct een trend zoeken in ieder punt van het seizoenspatroon. Als de seizoensgrootte bijvoorbeeld gelijk is aan 4, dan kunnen we kijken naar punten 0, 4, 8, 12, … . Deze punten komen overeen met alle eerste punten van het seizoen (de eerste kwartalen). We kunnen op zoek gaan naar een trend in die punten. Vervolgens kijken we naar punten 1, 5, 9, 13, … . Daar kunnen we ook een trend in vinden. Zo gaan we door tot we voor ieder punt van het seizoen een trendlijn hebben. De trendlijn kan met regressie worden bepaald.

We zoeken dus m trendlijnen. Voor ieder van die lijnen gebruiken we punten i+k⋅m waarbij i het nummer is van de trendlijn (i∈{0,...,m−1}) en k loopt van 0 tot en met ⌊(n−1−i)/m⌋. De x-coördinaten die met deze punten overeenkomen zijn gelijk aan i+k⋅m.

In ons voorbeeld is n=20 en m=4. We zoeken 4 trendlijnen waarbij we volgende punten gebruiken:

  • 0, 4, 8, 12, 16 met waarden 20, 37, 75, 92, 176

  • 1, 5, 9, 13, 17 met waarden 100, 136, 155, 202, 282

  • 2, 6, 10, 14, 18 met waarden 175, 245, 326, 384, 445

  • 3, 7, 11, 15, 19 met waarden 13, 26, 48, 82, 181

In Python kunnen we deze waarden als volgt vinden:

m = 4  # de periode gevonden met autocorrelatie

for i in range(n // m - 1):
    x = np.arange(i, opbrengsten.size, m)
    y = opbrengsten[x]
    print('{} met waarden {}'.format(x,y))

[ 0  4  8 12 16] met waarden [ 20.  37.  75.  92. 176.]
[ 1  5  9 13 17] met waarden [100. 136. 155. 202. 282.]
[ 2  6 10 14 18] met waarden [175. 245. 326. 384. 445.]
[ 3  7 11 15 19] met waarden [ 13.  26.  48.  82. 181.]

Nu moeten we voor elk van die lijnen de trendlijn vinden. Dit doen we met regressie. We doen dus m keer een regressie en stoppen al deze modellen in een lijst:

def find_regression_models(z: np.array, m: int, degree=1, exp=False):
    reg_models = []

    for i in range(z.size // m - 1):
        x = np.arange(i, opbrengsten.size, m).reshape(-1, 1)
        y = z[x]
        reg_models.append(GeneralRegression(degree, exp))
        reg_models[i].fit(x, y)

    return reg_models

# gebruik
models = find_regression_models(opbrengsten, m=4)

Merk op dat we de GeneralRegression klasse van het vorige hoofdstuk gebruiken. De parameters degree en exp worden ook meegegeven zodat je ook niet-lineaire regressie kan doen. Deze regressielijnen kunnen we dan gebruiken om voorspellingen te maken.

Volgende functie geeft ons het model voor de voorspelling:

from cursus.scripts import find_regression_models

def create_seasonal_trend_forecast(z: np.array, m: int, degree=1, exp=False):
    reg_models = find_regression_models(z, m, degree, exp)

    def forecast_function(x: np.array):
        predictions = np.empty(0)

        for i in range(x.size):
            y = reg_models[i % m].predict(x[i].reshape(1, -1))
            predictions = np.append(predictions, y)

        return predictions

    return forecast_function

array([246.6, 362. , 498.2, 279.6])

We zullen in dit voorbeeld kwadratische regressie nemen (deze geeft hier goede resultaten, bekijk zelf maar de alternatieven):

seasonal_trend_forecast = create_seasonal_trend_forecast(opbrengsten, 4, degree=2)
seasonal_trend_forecast(np.arange(20, 24))

We hebben nu een functie seasonal_predictor() die we kunnen gebruiken om te voorspellen. De voorspelde waarden voor het volgende jaar zijn:

predictions =  [246.6 362.  498.2 279.6]

We kunnen deze waarden als volgt plotten (we tekenen de regressielijnen erbij om de werking nog eens duidelijk te maken):

fig, ax = plt.subplots(figsize=(8, 5))

plot_trends(opbrengsten, np.hstack([np.repeat(np.nan, 20), predictions]), sub_title='Seasonal trend forecasting', ax=ax)

reg_models = find_regression_models(opbrengsten, m=4, degree=2)

for i in range(m):
   ax.plot(reg_models[i].predict(np.arange(24).reshape(-1, 1)), color='red', alpha=0.2)
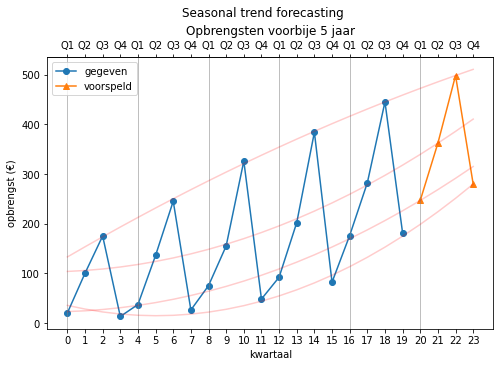
../_images/Forecasting_102_0.png

Ook kunnen we nu de betrouwbaarheid van deze voorspelling bepalen:

MAE RMSE MAPE
seasonal trend forecasting 6.188571 7.526714 0.090803
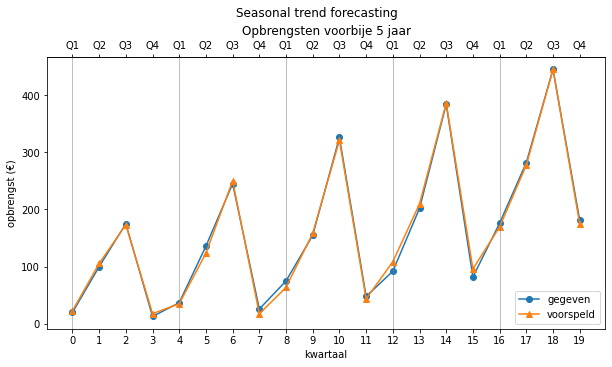
../_images/Forecasting_104_1.png

Dit is dus de beste voorspellingsmethode voor deze data, maar wederom moet je dit met een gigantische korreltje zout nemen, want dit model gebruikt nog meer gegevens (5 modellen in totaal) uit het verleden om datzelfde verleden te voorspellen. In Data Science 2 zullen we betere manieren zien om dit soort gegevens te voorspellen wanneer we het zullen hebben over neurale netwerken waarbij we rekening zullen houden met de echte voorspellende kracht van het neurale model.