Samenhang#

Causaliteit#

Verbanden zoeken tussen variabelen is een van de belangrijkste taken van een data-analist. In de pers kan je enorm veel gevonden verbanden vinden. Deze verbanden zijn eigenlijk een “correlatie”. Er zijn twee soorten: positieve en negatieve correlatie. Wanneer er een positieve correlatie bestaat tussen twee variabelen, wil dit zeggen dat een variabele stijgt als de andere variabele ook stijgt. Bij een negatieve correlatie daalt een variabele als de andere stijgt.

Een correlatie is in principe ook niets meer of minder dan deze vaststelling. In de praktijk gaat men er echter dikwijls vanuit dat er een causaal verband bestaat. Dit wil zeggen dat men ervan uitgaat dat de ene variabele afhankelijk is van de andere en dat we deze dus kunnen voorspellen aan de hand van de andere. Het is belangrijk te beseffen dat dit niet altijd het geval is. Een correlatie kan ook toevallig aanwezig zijn. Of er kan een andere connectie zijn.

Zo bestaat er een correlatie tussen het aantal zakkenrollers en het aantal ijsjes die verkocht worden. Het is echter niet zo dat het aantal verkochte ijsjes de oorzaak is van het aantal zakkenrollers. In dit geval hebben de twee zaken een gemeenschappelijke oorzaak: de aanwezigheid van veel mensen tijdens een dag met goed weer.

Sommige correlaties kunnen ook puur toevallig zijn. Zo bestaat er een correlatie tussen het aantal films met Nicolas Cage en het aantal mensen die verdrinken in een zwembad. Zie ook:

http://www.tylervigen.com/spurious-correlations.

Het voorbeeld#

We zullen de begrippen en de werkwijzen in dit document illustreren met een voorbeeld. In dit voorbeeld hebben we aan 2064 mensen gevraagd wat hun bruto loon is en hoeveel LinkedIn connecties ze hebben. We vragen ons af of er een verband tussen de twee bestaat.

Het resultaat van deze enquête is een tabel met als variabelen loon en connecties.

	loon	connecties
0	3252	304
1	2968	216
2	2976	159
3	3255	273
4	1953	191

In dit geval zijn er geen uitschieters of NaN-waarden. Er zijn ook geen ordinale variabelen (alle variabelen hebben ratio meetniveau). Dus hoeven we deze niet speciaal te behandelen.

Er is een eenvoudige manier om al te weten te komen of er mogelijk een correlatie is. Dit doen we met een “scatterplot”. Voor iedere rij in de tabel wordt het aantal connecties gebruikt als x-coördinaat en het loon als y-coördinaat. Iedere lijn correspondeert dan met een punt in een vlak. We kunnen deze punten in Python tekenen met:

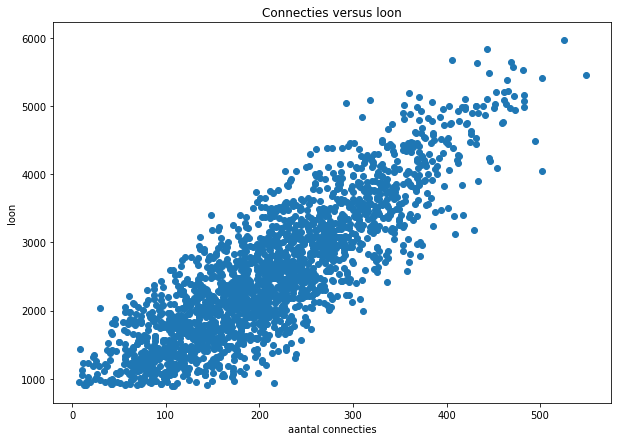
Er ontstaat dus een “wolk” van punten. In deze grafiek kan je zien dat er hoogst waarschijnlijk wel een verband is. Hoe hoger het aantal connecties, hoe hoger het loon. Maar er zit natuurlijk ook wel wat variatie op. Als het verband perfect zou zijn, dan zou er een rechte lijn ontstaan in de grafiek.

Is er een causaal verband? Dat zou willen zeggen dat het aantal connecties je loon bepaalt. En dus zou je meer kunnen verdienen door veel requests te sturen naar andere mensen. Dat is (hopelijk) duidelijk niet het geval. Nochtans is het verband wel te verklaren: mensen met een hoog loon zijn dikwijls mensen in een hoge functie en die hebben over het algemeen een groter netwerk. Mensen met een groot netwerk zullen waarschijnlijk ook sneller in een hogere functie geraken, maar dat wordt hier niet bewezen!

Een scatterplot is in elk geval een heel goede techniek om snel te zien of er een mogelijk verband bestaat tussen 2 variabelen. Het geeft echter geen kwantitatief resultaat (je kan niet zeggen hoe groot of klein het verband is). We hebben dus nood aan een maat voor de correlatie. Dat bespreken we hieronder.

Correlatiecoëfficiënt van Pearson#

Om een waarde te kunnen plakken op de mate van correlatie, hebben we een formule nodig. De gebruikte formule hangt af van het meetniveau van de variabelen. Als het meetniveau minstens interval is, kunnen we de correlatie bijvoorbeeld berekenen aan de hand van de formule van Pearson.

Deze formule zet de 2 kolommen eerst om naar Z-scores. Z-scores bekom je door alle waarden te verminderen met het gemiddelde van die waarden en dan te delen door de standaardafwijking van die waarden. In Python kan je Z-scores van alle kolommen in een dataframe vinden met de functie:

Het resultaat van deze bewerking is dat alle kolommen 0 als gemiddelde hebben en 1 als standaardafwijking. Omzetten naar Z-scores gebeurt heel dikwijls als je variabelen wil vergelijken die veel in grootte verschillen. Het zet alle variabelen om naar dezelfde schaal.

Daarna worden alle Z-scores per paar met elkaar vermenigvuldigd en daarvan wordt het gemiddelde genomen. Wiskundig gebeurt er dit:

c o r (x, y) = r_{x y} = \frac{1}{n} \sum_{i = 1}^{n} Z x_{i} \cdot Z y_{i} = \frac{1}{n} \sum_{i = 1}^{n} \frac{x_{i} - \overset{―}{x}}{s_{x}} \cdot \frac{y_{i} - \overset{―}{y}}{s_{y}}

In Python kan je dit handmatig berekenen met:

c = (linkedin_scaled.loon * linkedin_scaled.connecties).mean()
print(c)

0.854603892685227

Maar er bestaat ook een ingebouwde functie die dit doet:

c = linkedin.connecties.corr(linkedin.loon)
print(c)

0.8546038926852271

Zoals je ziet komt er een getal uit dat de correlatie weergeeft. De volgorde van de twee parameters speelt geen rol. Als je ze omdraait, krijg je dezelfde waarde.

Het bekomen getal ligt altijd tussen -1 en 1. Als de correlatie gelijk is aan 1, dan liggen de punten allemaal op een perfect, stijgende lijn. Als de correlatie gelijk is aan -1, dan liggen de punten ook op een lijn, maar dan daalt deze. De helling van de lijn speelt daarbij geen rol. De absolute waarde van de correlatie zegt dus hoe goed de correlatie is.

Als de punten minder op een lijn liggen, dan zal deze absolute waarde dalen. Als er helemaal geen verband is, dan krijg je het getal 0. In volgend overzicht (van wikipedia) zie je een aantal voorbeelden:

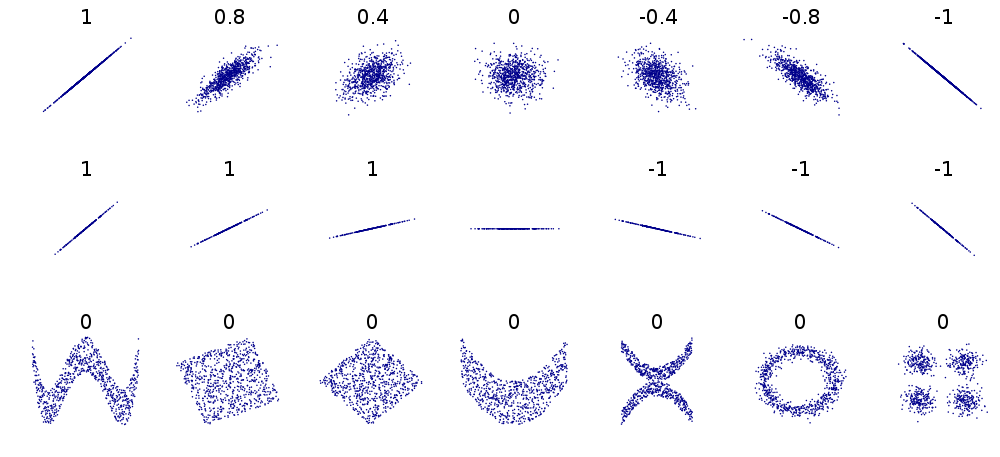
De bovenste rij voorbeelden kom je dikwijls tegen. De tweede rij illustreert dat de helling van de lijn geen rol speelt in het resultaat.

De laatste rij laat zien dat de correlatie 0 kan zijn terwijl er toch een verband is. Dit is een heel belangrijke vaststelling! De correlatiecoëfficiënt van Pearson zoekt namelijk naar een “lineair verband”. Dit wil zeggen dat er wordt nagegaan in hoeverre er een rechte lijn door de punten gaat. Het kan dus zijn dat er geen rechte lijn door gaat, maar wel een andere. Dat kan je niet op deze manier meten.

Hoe interpreteren we de gevonden waarde nu? Als de waarde positief is, dan spreken we van een “positieve correlatie” en als de waarde negatief is, spreken we van een “negatieve correlatie”. De absolute waarde van het gevonden getal geeft dan de mate waarin dit verband bestaat. Daar is veel ruimte voor interpretatie en veel hangt af van de context waarin je werkt.

Stel dat je experimenten doet in de scheikunde en het verband zoekt tussen de hoeveelheid van een bepaalde stof en de temperatuur van de reactie, dan spreken we pas van een duidelijk verband als de correlatie hoger is dan 0,99. Als de correlatie lager is, dan duidt dit op fouten of de aanwezigheid van andere factoren (de meting was dan dus onbetrouwbaar).

In de sociale wetenschappen is de situatie echter helemaal anders. Daar zoekt men bijvoorbeeld het verband tussen de tevredenheid van een werknemer en de hoeveelheid stress die die ervaart. Dat is enorm moeilijk te meten. Er zijn namelijk heel veel factoren die de tevredenheid en de stress beïnvloeden en een groot deel is subjectief. Als je dan een correlatie vindt van 0,5 kan je al heel tevreden zijn.

In de IT sector worden meestal metingen gedaan in verband met netwerkbelasting en serverbelasting. Deze zaken zijn redelijk betrouwbaar te meten, maar ook daar spelen allerlei factoren een rol. Vandaar dat we volgende afspraken maken:

Correlatie	betekenis
0	geen enkel lineair verband
0 tot 0,2	nauwelijks lineair verband
0,2 tot 0,4	zwak lineair verband
0,4 tot 0,6	redelijk lineair verband
0,6 tot 0,8	sterk lineair verband
0,8 tot 1	zeer sterk lineair verband

Zoals je ziet zijn deze begrippen redelijk vaag, maar jammer genoeg kan je geen duidelijkere benamingen geven. In de praktijk zijn we in de IT sector vooral geïnteresseerd als de correlatie hoger is dan 0,6.

De gevonden correlatie (0,85) is dus heel hoog. We zeggen dat er een zeer sterk lineair verband bestaat tussen het aantal LinkedIn connecties en het brutoloon.

Rangcorrelatie#

Om de correlatiecoëfficiënt van Pearson te berekenen, moeten de variabelen minstens interval meetniveau hebben. Dat was ook het geval bij het LinkedIn voorbeeld. Maar soms zijn de variabelen ordinaal. We kunnen dan nog steeds spreken van waarden die stijgen of dalen, maar de waarde zelf heeft geen betekenis meer en we kunnen er in principe dus ook niet mee rekenen.

Als de waarden ordinaal zijn, kunnen we ook nog een correlatie bepalen. Deze zal dan aangeven of de y-waarden stijgen als de x-waarden stijgen (positieve correlatie). Of andersom: of de y-waarden dalen wanneer de x-waarden stijgen ( negatieve correlatie).

Een voorbeeld moet dit duidelijk maken. Stel dat de LinkedIn enquête als volgt werd ingevuld. Het aantal connecties kan enkel een van volgende waarden aannemen: “weinig”, “matig”, “gemiddeld”, “meer”, “veel”, “extreem veel”. Het loon kan dan weer een van volgende waarden zijn: “klein”, “modaal”, “groot”, “extreem”. Volgende code zet de waarden van de enquête om naar dit systeem:

connectiesCutpoints = [0, 30, 150, 250, 300, 400, 600]
connectiesCategories = ["weinig", "matig", "gemiddeld", "meer", "veel", "extreem veel"]
loonCutpoints = [0, 2000, 3000, 5000, 6000]
loonCategories = ['klein', 'modaal', 'groot', 'extreem']
connecties = pd.cut(linkedin.connecties, bins=connectiesCutpoints)
connecties.cat.categories = connectiesCategories
loon = pd.cut(linkedin.loon, bins=loonCutpoints)
loon.cat.categories = loonCategories

Zoals je kan zien zijn de categorieën onregelmatig. Het verschil tussen “weinig” en “matig” is niet gelijk aan het verschil tussen “matig” en “gemiddeld”. Enkel de volgorde is nog juist.

Als we nu een verband zoeken, kunnen we niet meer rekenen. We bespreken 2 methoden om toch een correlatie te vinden: Kendall en Spearman. Bij beide methodes worden de waarden eerst omgezet naar rangnummers. Een rangnummer bepaalt per waarde op welke plaats deze zou komen indien de rij gesorteerd zou worden. De kleinste waarde krijgt rangnummer 1 en de grootste waarde krijgt rangnummer n (als er n getallen zijn).

Een klein voorbeeldje moet dit duidelijk maken. Stel dat je de waarden 10, 5, 12 en 1 in een variabele hebt, dan zijn de rangnummers: 3, 2, 4, 1. De laatste waarde is de kleinste (deze heeft rang 1), de tweede waarde is de tweede-kleinste (rangnummer 2), de eerste waarde is de derde-kleinste (rangnummer 3) en de derde is de grootste waarde (rangnummer 4).

In Python kan je dit vinden met de rank()-functie:

voorbeeld = pd.DataFrame([10, 5, 12, 1])
print(voorbeeld.rank())

Toegepast op de lonen en de connecties:

loonRang = loon.rank()
connectiesRang = connecties.rank()

Aangezien de waarden van deze rangnummers geen betekenis meer hebben, is het begrip “lineair” verband ook niet zinvol. De volgende technieken kunnen dus ook een hoge correlatie geven wanneer er een niet-lineair verband is. Daardoor kan het dus interessant zijn om deze maten te gebruiken, ook al hebben de variabelen een interval of ratio meetniveau.

Spearman#

De techniek van Spearman is eigenlijk heel eenvoudig: zet de waarden om naar rangnummers en bereken de Pearson correlatiecoëfficiënt zoals hiervoor beschreven.

Deze methode is heel eenvoudig, maar misbruikt dus de waarden van de rangen door ze te interpreteren als getallen met minstens interval meetniveau.

Als je dit in Python wil doen, dan werk je als volgt:

loonRang = loon.rank()
connectiesRang = connecties.rank()
connectiesRang.corr(loonRang)

0.7626941369403833

De interpretatie van deze waarde is gelijk aan de Pearson coëfficiënt. Zoals je ziet is de correlatie nog steeds vrij hoog.

Kendall#

De methode van Spearman is niet helemaal correct. We rekenen namelijk met de getallen die in feite geen getallen zijn, maar rangnummers. Als we de berekening juist willen doen, moeten we dus kijken of waarden hoger of lager zijn, maar geen rekening houden met de waarde van het verschil.

Dat gebeurt in de methode van Kendall. Bij deze methode worden alle combinaties van $x_{i}$ en $x_{j}$ vergeleken met de overeenkomende $y_{i}$ en $y_{j}$ waarden. Er wordt steeds gekeken of er een stijging of daling is bij de x-waarden en of dat dit ook het geval is bij de y-waarden. Er wordt dan geteld hoeveel stijgingen (of dalingen) overeenkomen en hoeveel er niet overeenkomen. De werkwijze is als volgt:

import numpy as np

def kendall(x, y):
    x = x.rank()
    y = y.rank()
    n = len(x)
    aantal = 0

    for i in range(1, n - 1):
        for j in range(i + 1, n):
            aantal = aantal + np.sign(x[i] - x[j]) * np.sign(y[i] - y[j])

    return 2 * aantal / (n / (n - 1))

Bovenstaande berekening werkt enkel als er geen dubbels voorkomen bij de $x_{i}$ en de $y_{i}$ waarden. In de praktijk is dit echter meestal wel het geval. Het algoritme wordt dan aangepast om daarmee rekening te houden. We zullen in dit document de details daarvan weg laten. We kunnen de correlatie namelijk gemakkelijk in Python berekenen met:

connectiesRang.corr(loonRang, method='kendall')

0.6991211582823866

Wederom is er een sterk verband aangetoond tussen de twee variabelen.

Lineaire regressie#

Wanneer een sterk lineair verband wordt vastgesteld (door een scatterplot en/of een hoge correlatie), dan wil dit zeggen dat de punten nagenoeg op een rechte lijn liggen. We kunnen deze lijn dus ook proberen te vinden. Die lijn kunnen we dan gebruiken als een model om de ene variabele te voorspellen aan de hand van de andere. De volgorde is hier belangrijk en daarom gebruiken we 2 benamingen voor de variabelen:

de “onafhankelijke variabele” is de variabele die we willen gebruiken om de andere te voorspellen
de “afhankelijke variabele” is de variabele die we willen voorspellen aan de hand van de andere

Bemerk dat je pas over een lijn kan spreken als de variabelen beiden minstens interval meetniveau hebben!

Het bepalen van de lijn#

Als er een rechte lijn door de punten gaat, dan heeft deze de volgende vergelijking:

y = a + b \cdot x

waarbij $x$ de onafhankelijke variabele is en $y$ de afhankelijke. De waarde van $a$ noemt men ook wel de “intersectie”. Deze bepaalt de hoogte van de lijn. De waarde van $b$ is de “richtingscoëfficiënt” en bepaalt de helling van de lijn. De waarden van $a$ en $b$ bepalen dus de lijn.

We willen de waarden van $a$ en $b$ vinden zodat de lijn “zo goed mogelijk” door de punten gaat. Dit wil eigenlijk zeggen dat het verschil tussen de lijn en de echte waarden zo klein mogelijk moet zijn. We kunnen dit als volgt berekenen:

s_{e} = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} (y_{i} - (a + b \cdot x_{i}))^{2}}

Bemerk dat deze formule enorm lijkt op die van de standaardafwijking. We berekenen de gemiddelde afwijking tussen de echte y-waarden en de voorspelde y-waarde door de lijn. Het resultaat is een getal dat aangeeft hoe goed de lijn door de punten gaat (de gemiddelde fout die de lijn maakt tegenover de punten). Hoe kleiner de waarde, hoe beter de lijn erdoor gaat. Men noemt deze waarde de “standaard schattingsfout”.

Als we $a$ en $b$ kennen zouden we dit als volgt in Python kunnen berekenen:

import math as m

a = 1
b = 2
x = linkedin.connecties
y = linkedin.loon
voorspeld = a + b * x
fout = y - voorspeld
se = m.sqrt((fout ** 2).mean())

De waarde van $s_{e}$ is afhankelijk van $a$ en $b$ . We zoeken nu dus de waarden van $a$ en $b$ zodat de waarde van $s_{e}$ zo klein mogelijk is. Grafisch zou je dit als volgt kunnen zien:

Image('images/minimum_zoeken.png')

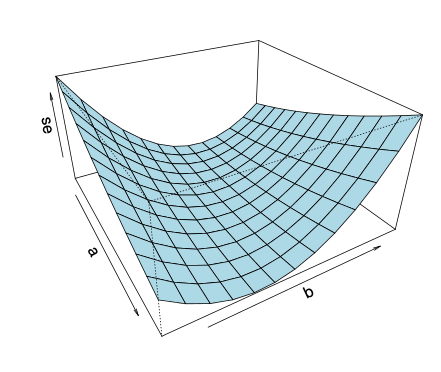
Voor iedere waarde van $a$ en $b$ , vinden we een $s_{e}$ en we zoeken waarden zodat $s_{e}$ zo klein mogelijk is.

Gelukkig hoef je niet alle combinaties van $a$ en $b$ te doorlopen. Wiskundigen hebben formules bepaalt die de waarden exact berekenen. Deze zijn als volgt:

b = r_{x y} \cdot \frac{s_{y}}{s_{x}} e n a = \overset{―}{y} - b \cdot \overset{―}{x}

Hierbij is $r_{x y}$ gelijk aan de correlatiecoëfficiënt van Pearson. $s_{x}$ en $s_{y}$ zijn respectievelijk de standaardafwijkingen van $x_{i}$ en $y_{i}$ . En $\overset{―}{x}$ en $\overset{―}{y}$ zijn respectievelijk de gemiddelden van $x_{i}$ en $y_{i}$ .

Regressie in Python#

Je kan de waarden van $a$ en $b$ vinden via lineaire regressie. In Python zijn er verschillende manieren om regressie toe te passen. Een zeer goede bibliotheek is Scikit Learn, die we trouwens ook voor clustering zullen gebruiken. Je werkt als volgt:

Je importeert de data en zet alles om naar een numpy array d.m.v. to_numpy(). De inputs noem je X en de outputs noem je y. De hoofdletter wijst erop dat het vaak om meerdere kolommen gaat.
Vervolgens doe je op de X data een transformatie m.b.v. .reshape(-1,1), en op de target data y is dit niet nodig.

from sklearn import linear_model

X = linkedin.connecties.to_numpy().reshape(-1, 1)
y = linkedin.loon.to_numpy()
regr = linear_model.LinearRegression()
model = model.fit(X, y)
print(model)

LinearRegression()

Je vindt de intercept terug d.m.v. model.intercept_. In dit model hebben we maar 1 variabele voor x, maar in veel gevallen heb je meerdere variabelen $x_{1}$ , $x_{2}$ , $x_{3}$ ,…die y gaan bepalen. De coefficient voor iedere variabele vinden we terug in de array: model.coef_

a = model.intercept_
b = model.coef_[0]
print(f'a={a}')
print(f'b={b}')

a=651.6435845707622
b=8.913063980115949

Als je nu een voorspelling wil doen aan de hand van deze lijn, gebruik je de vergelijking van de rechte. Bijvoorbeeld: stel dat we het loon willen kennen voor iemand met 200 connecties:

a + b * 200

2434.2563805939517

In praktijk zullen we steeds de predict-methode van het model gebruiken. Stel dat we voor de waarden 200 en 300 het loon willen voorspellen. Het gaat als volgt:

X_nieuw = np.array([200, 300]).reshape(-1, 1) # de reshape maakt van de rijvector een kolomvector
print(X_nieuw)
model.predict(X_nieuw)

Xnieuw = 
[[200]
 [300]]

array([2434.25638059, 3325.56277861])

Dit is maar een schatting. Om te weten hoe goed de schatting is, berekenen we de waarde van $s_{e}$ :

se = m.sqrt(((model.predict(X) - y) ** 2).mean())
print(se)

511.33018125890214

De lijn wijkt dus gemiddeld 511 EUR af van de gegeven punten. Dat is een vrij hoge waarde als je weet dat de lonen tussen 900 en 6000 EUR liggen. Het echte loon van iemand met 200 connecties zal dus waarschijnlijker tussen 2434-511 ( 1923) en 2434+511 (2945) EUR liggen.

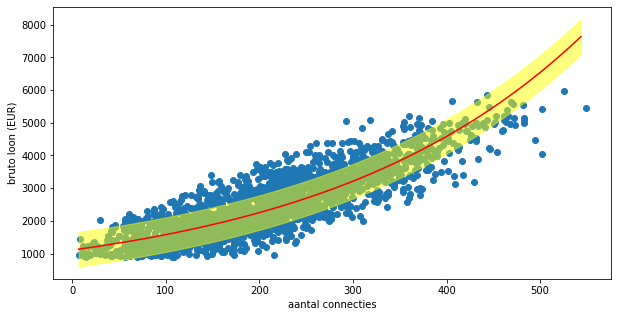
Als je dit grafisch wil tonen, kan je volgende code gebruiken:

fig, ax = plt.subplots(figsize=(12, 8))
_ = ax.scatter(X, y)
xx = np.arange(X.min(), X.max(), (X.max() - X.min()) / 100)
yy = model.predict(xx.reshape(-1, 1))
_ = ax.fill_between(xx, yy - se, yy + se, color="yellow", alpha=0.2)
_ = ax.plot(xx, yy, color='red')
_ = ax.set_xlabel("aantal connecties")
_ = ax.set_ylabel("bruto loon (EUR")
plt.show()

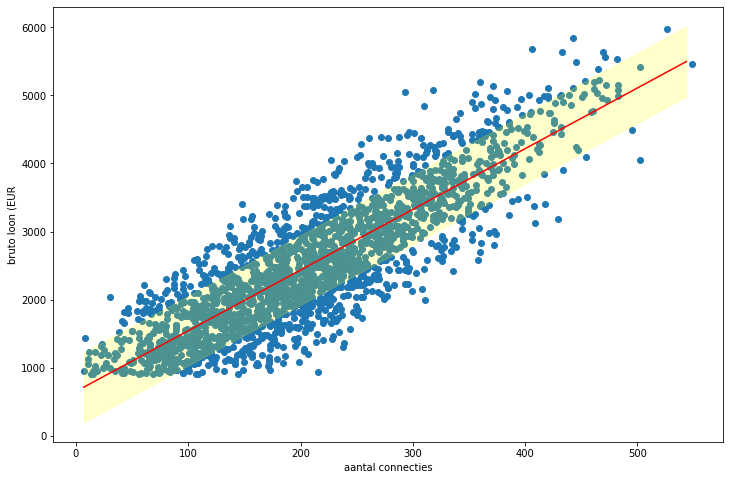
Hierboven zie je de regressielijn met daarrond de foutmarge volgens de waarde van 𝑠𝑒.

Verklaarde variantie#

De waarde van $s_{e}$ geeft aan wat de gemiddelde fout is wanneer je de lijn gebruikt om het loon te voorspellen. Maar die waarde heeft pas zin als je weet in welke grootte orde de lonen liggen.

Vandaar dat men dikwijls nog een andere maat gebruikt om te weten hoe goed de voorspelling is. Om die te construeren, kijken we naar de formule van $s_{e}$ :

s_{e} = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} (y_{i} - (a + b \cdot x_{i}))^{2}}

Als we in deze formule de waarden van $a$ en $b$ invullen, dan vinden we (na veel rekenwerk):

s_{e} = s_{y} \cdot \sqrt{1 - r_{x y}^{2}}

Als we beide kanten kwadrateren, vinden we:

s_{e}^{2} = s_{y}^{2} \cdot (1 - r_{x y}^{2})

Als $r_{x y}^{2} = 0$ , dan is er geen correlatie tussen $x$ en $y$ . De waarde van $s_{e}^{2}$ is dan exact gelijk aan die van $s_{y}^{2}$ . Dat wil zeggen dat de fout die je maakt bij een voorspelling even groot is dan de variantie die er op de y-waarden zit.

Als $r_{x y}^{2} = 1$ , dan is er een perfecte correlatie tussen $x$ en $y$ . De waarde van $s_{e}^{2}$ is dan 0 (we maken dus geen fout meer door een voorspelling te doen).

Als $r_{x y}^{2} = 0, 8$ , dan is de waarde van $s_{e}^{2}$ gelijk aan 20% van de variantie in de y-waarden. Dat wil dus zeggen dat het model (de lijn die we gebruiken) voor 80% bijdraagt aan de werkelijke waarde. 20% wordt niet verklaard door het model (er is dus waarschijnlijk nog een andere factor die bijdraagt aan de werkelijke waarde).

De waarde van $r_{x y}^{2}$ geeft dus het percentage weer waarin de onafhankelijke variabele een rol speelt in het voorspellen van de afhankelijke variabele. Deze waarde noemt men dikwijls de “verklaarde variantie” en wordt weergegeven met het symbool $R^{2}$ . Hoe hoger deze waarde, hoe beter het model.

In Python kan je deze waarde als volgt vinden:

# als pandas series via corr
r_squared = linkedin.connecties.corr(linkedin.loon) ** 2
print(r_squared)
# of via numpy corrcoef
r_squared = np.corrcoef(linkedin.loon.to_numpy(), linkedin.connecties.to_numpy()) ** 2
print(r_squared)

0.7303478133927431
[[1.         0.73034781]
 [0.73034781 1.        ]]

In ons geval zien we dus dat het aantal connecties voor 73% een rol speelt in het loon dat iemand krijgt. De overige 27% is te wijten aan andere factoren (die we hier niet kunnen bepalen).

Niet-lineaire regressie#

Soms kan je geen rechte lijn trekken, maar wel een andere. Zo kunnen de gegevens op een parabool liggen of kan er een exponentieel verband zijn of een logaritmisch of nog een ander.

De werkwijze bij niet-lineaire regressie is heel gelijklopend aan lineaire regressie: je start met een vergelijking van de lijn en zoekt dan de waarden van de parameters in die vergelijking zodat de lijn zo goed mogelijk door de punten gaat. Het zoeken naar de juiste waarden gebeurt hier echter niet meer exact. Meestal zal de computer starten bij bepaalde waarden en deze laten evolueren naar de optimale waarden. Je kan dit vergelijken met een bal die je op het oppervlak legt en die je naar beneden laat rollen.

Hier zie je een aantal voorbeelden van veel voorkomende lijnen:

kwadratisch: $y = a + b \cdot x + c \cdot x^{2}$
kubisch: $y = a + b \cdot x + c \cdot x^{2} + d \cdot x^{3}$
logaritmisch: $y (x) = a \cdot l n (x) + b$
exponentieel: $y = e^{a + b \cdot x}$
…

Om de waarden van $a$ , $b$ , $c$ en $d$ te bepalen, kunnen we Python gebruiken. We definiëren een klasse voor ons algemeen model:

from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error, r2_score as r2score


class GeneralRegression:
    def __init__(self, degree=1, exp=False, log=False):
        self.degree = degree
        self.exp = exp
        self.log = log
        self.model = None
        self.x_orig = None
        self.y_orig = None
        self.X = None
        self.y = None

    def fit(self, x, y):
        self.x_orig = x
        self.y_orig = y
        self.X = x

        if self.exp:
            self.y = np.log(y)

        else:
            self.y = y

        if self.log:
            self.X = np.log(self.X)

        self.model = make_pipeline(PolynomialFeatures(degree=self.degree), LinearRegression())
        self.model.fit(self.X, self.y)

    def predict(self, x):
        X = x

        if self.exp:
            return np.exp(self.model.predict(X))

        if self.log:
            return self.model.predict(np.log(X))

        return self.model.predict(X)

    @property
    def r2_score(self):
        return r2score(self.y_orig, self.predict(self.x_orig))

    @property
    def se_(self):
        if self.exp:
            return mean_squared_error(self.predict(self.X), np.exp(self.y), squared=False)
        if self.log:
            return mean_squared_error(self.predict(self.X), np.log(self.y), squared=False)
        return mean_squared_error(self.predict(self.X), self.y, squared=False)

    @property
    def coef_(self):
        return self.model.steps[1][1].coef_

    @property
    def intercept_(self):
        return self.model.steps[1][1].intercept_

Je gebruikt GeneralRegression zoals LinearRegression van sklearn. Alleen hoef je geen reshape(-1,1) uit te voeren op de X-waarden dit wordt in de bovenstaande code reeds voor ons gedaan. Bij het definieren van het model geef je de juiste parameters mee:

degree: de graad van de polynoom dat je gaat “fitten” (1=lineair 2=kwadratisch, 3=kubisch, …)
exp: een boolean die aangeeft of je een exponentiële kromme zoekt
log: een boolean die aangeeft of je een logaritmische kromme zoekt

Bijvoorbeeld:

We trachten een derde graadspolynoom te fitten: $y = a + b \cdot x + c \cdot x^{2} + d \cdot x^{3}$

dan kan dit met deze code:

model3 = GeneralRegression(degree=3)
linkedin2 = linkedin[linkedin.connecties > 2]
model3.fit(linkedin.connecties.to_numpy(), linkedin.loon.to_numpy())
print(model3.r2_score)

print(f"De standaard error se= {model3.se_}")
print(f"De waarden van a, b, c en d zijn respectievelijk {model3.intercept_, model3.coef_[1], model3.coef_[2], model3.coef_[3]}")

0.73700607748326
De standaard error se = 504.978
De waarden van a, b, c en d zijn respectievelijk 1118.43, 2.6002, 0.022656, -0.0000224602

De vergelijking is dus: $y = 1118, 43 + 2.6002 \cdot x + 0.022656 \cdot x^{2} - 0, 0000224602 \cdot x^{3}$ Je ziet dat de waarden voor c en d redelijk klein zijn. Dat komt omdat de gegevens een lineair verband hebben. Een hogere graad van regressielijn levert daarom weinig op. Dat kan je zien aan de waarden van $s_{e}$ en $R^{2}$ . Die liggen zeer dicht bij die van lineaire regressie. Dit model is theoretisch gezien wel iets beter, maar de complexiteit die je ervoor in ruil geeft is het niet waard. Als je de curves doortrekt, zal je ook zien dat de hogere graad juist slechtere resultaten zal opleveren. Als je wil weten hoeveel loon iemand met 200 connecties heeft, volgens dit model, dan kan je dat als volgt zien:

# we voorspellen bijvoorbeeld de waarde voor 0,1, -200 en 300
loon = model3.predict(np.array([200]))
print(f"Het voorspelde loon voor 200 connecties is {loon[0]}")

Het voorspelde loon voor 200 connecties is 2365.029

Dit ligt inderdaad dicht bij de waarde die we vonden bij lineaire regressie. Exponentiële regressie pas je best toe op gegevens die ook exponentieel van aard zijn. Je kan echter altijd een meest optimale lijn vinden. Als we dat hier doen, dan krijg je:

model_exp = GeneralRegression(degree=1, exp=True)
model_exp.fit(linkedin.connecties.to_numpy(), linkedin.loon.to_numpy())
print(f"De standaard error se= {model_exp.se_}")
print(f"De waarden van a, b zijn respectievelijk {model_exp.intercept_, model_exp.coef_[1]}")

De standaard error se = 529.452
De waarden van a, b zijn respectievelijk 7.00858, 0.00355438

De formule is hier dus $y = e^{7.00858 + 0.00355438 \cdot x}$ . De waarden van $s_{e}$ en $R^{2}$ zijn nu wel slechter dan die van lineaire regressie. Het loon van iemand met 200 connecties volgens dit model is nu:

model_exp.predict(np.array([200]))

array([2251.72225935])

Je kan de regressielijn ook tekenen in een plot. Daartoe maken we volgende functie:

def plot_regressionline(model, min, max, linecol="red", errorcol="#FFFF0080"):
    se = model.se_
    predict = model.predict(linkedin.connecties.to_numpy())
    x = np.arange(min, max, (max - min) / 100)
    y = model.predict(x)
    plt.fill_between(x, y - se, y + se, color=errorcol)
    plt.plot(x, y, color=linecol)


# Deze functie kan je gebruiken in een figuur. Bijvoorbeeld als volgt:
_ = plt.figure(figsize=(10, 5))
_ = ax = plt.axes()
_ = ax.scatter(x, y)
plot_regressionline(model3, x.min(), x.max())
_ = ax.set_xlabel("aantal connecties")
_ = ax.set_ylabel("bruto loon (EUR)")
_ = plt.show()

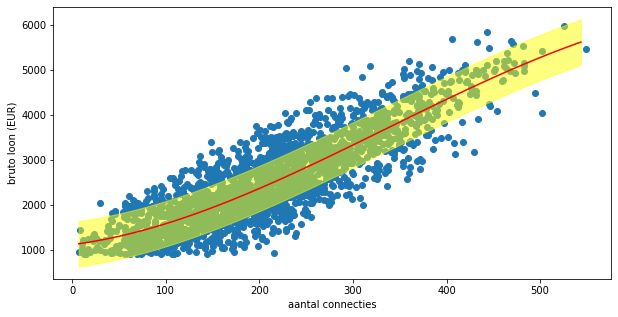
Deze functie kan je gebruiken in een figuur. Bijvoorbeeld als volgt:

_ = plt.figure(figsize=(10, 5))
_ = ax = plt.axes()
_ = ax.scatter(x, y)
plot_regressionline(model_exp, x.min(), x.max())
_ = ax.set_xlabel("aantal connecties")
_ = ax.set_ylabel("bruto loon (EUR)")
_ = plt.show()

Data Science 1

Samenhang

Contents